给定一个数据序列,在某个时间点,数据的某个(或某些)参数可能由于系统性因素(而非偶然性因素)而突然发生变化,那么这个时间点被称为变点(changepoint)。变点检测(changepoint detection)就是要估计出变点的位置。
本文主要打算理一下这篇论文:
Bayesian Online Changepoint Detection. Ryan Prescott Adams and David J.C. MacKay. arXiv 2007. [Paper]
翻译过来大概是贝叶斯在线变点检测?“online”这个词指检测变点时只能利用当前已经观测到的数据,不能用未来数据。而很多 offline 的方法是可以拿所有的数据来做检测的。
本文很大程度上(又)抄参考了一篇讲 BOCD 讲得非常清楚的博客:
Bayesian Online Changepoint Detection (Gregory Gundersen)
问题定义
假设有一个观测序列 x1,x2,…,xT∈Rd,我们用 xa:b 来表示 xa,xa+1,…xb。x1:T 可以被划分成一些不重叠的 product partitions,即每个 partition 中的数据点都是 i.i.d(独立同分布)的,都服从参数为 θp 的分布 p(xt∣θp),每个 partition 的参数 θp∼p(ϕ) 也是 i.i.d 的:
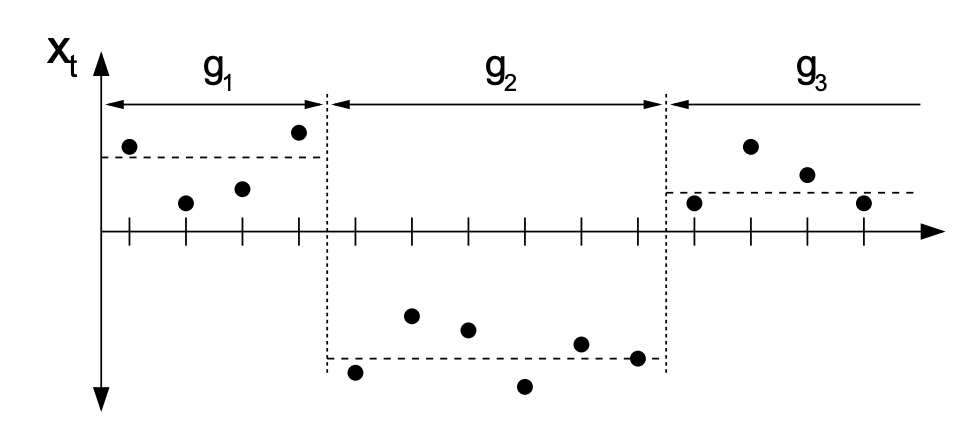
而 BOCD 会估计当前时刻的 run length(距离上一个变点已经过了多少时刻)的后验分布 p(rt∣x1:t),t 时刻的 run length 为 rt。显然 rt 只可能有两种情况:
x={0rt−1+1t 时刻是变点t 时刻不是变点
那么一个可能的 rt 随 t 的变化图如下(rt=0 的时刻(t=5,11)为变点):
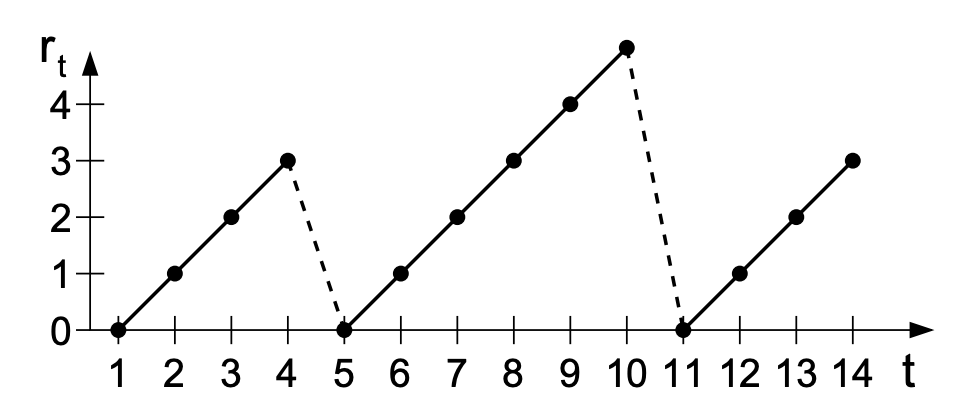
除了 p(rt∣x1:t) 以外,BOCD 还会估计 p(xt+1∣x1:t),这样就能既预测变点(run lenght),又预测下一个数据点的值了。不过如果单纯只求变点的话,p(xt+1∣x1:t) 是没必要算的。
一个递推式
如果不想看推导过程,可以直接跳到这里看结果。
下一个数据点的分布
p(xt+1∣x1:t) 可以由给定 rt 时 xt+1 的边缘分布算出来:
p(xt+1∣x1:t)=rt∑p(xt+1,rt∣x1:t)=rt∑p(xt+1∣rt,x1:t)p(rt∣x1:t)=r=0∑tp(xt+1∣rt=r,x(t−r):t)p(rt∣x1:t)=rt∑p(xt+1∣rt,xt(r))p(rt∣x1:t)(边缘概率公式)(链式法则)(假设 1)
其中 xt(r)=x(t−r):t 为 run length =r 时当前 partion 的观测点集合,因为我们只会用当前 partion 的数据来预测 xt+1 的分布(假设 1)。因为 rt 可能为 0,所以 xt(r) 可能为空集。
run length 的分布
那么我们就需要计算 run length 的分布 p(rt∣x1:t):
p(rt∣x1:t)=p(x1:t)p(rt,x1:t)
那么我们需要算联合概率 p(rt,x1:t):
p(rt,x1:t)=rt−1∑p(rt,rt−1,x1:t)=rt−1∑p(rt,rt−1,x1:t−1,xt)=rt−1∑p(rt,xt∣rt−1,x1:t−1)p(rt−1,x1:t−1)=rt−1∑p(xt∣rt,rt−1,x1:t−1)p(rt∣rt−1,x1:t−1)p(rt−1,x1:t−1)=rt−1∑p(xt∣rt−1,x(r))p(rt∣rt−1)p(rt−1,x1:t−1)(边缘概率公式)(链式法则)(链式法则)(假设 1, 2)
最后一步能成立依赖于以下两个假设:
- 前面提到的假设 1,即只用当前 partion 的数据来预测 xt 的分布:
p(xt∣rt,rt−1,x1:t−1)=p(xt∣rt−1,xt−1(r))(假设 1)
因为 rt 只依赖于 rt−1(假设 2),所以这里 rt 也可以省掉。
- rt 只依赖于 rt−1。即给定 rt−1,rt 对其他所有变量都条件独立:
p(rt∣rt−1,x1:t−1)=p(rt∣rt−1)(假设 2)
递推流程
可以看到求 p(xt+1∣x1:t) 的过程是一个递推的过程。在 t 时刻,p(rt−1,x1:t−1) 已经计算出来了,现在我们要求 p(xt+1∣rt,xt(r)),那么计算流程为:
-
计算变点的先验 p(rt∣rt−1)
-
计算 run length rt 的后验分布:p(rt∣x1:t)=p(x1:t)p(rt,x1:t)
其中:
p(rt,x1:t)=rt−1∑UPMp(xt∣rt−1,xt−1(r))变点先验p(rt∣rt−1)已求得的信息p(rt−1,x1:t−1)
- 计算新数据点的分布 p(xt+1∣x1:t):
p(xt+1∣x1:t)=rt∑UPMp(xt+1∣rt,xt(r))已求得的信息p(rt∣x1:t)
可以看到,我们还需要计算的两个式子是:
-
p(xt∣rt−1,xt−1(r)) 和 p(xt+1∣rt,xt(r)):为了方便,我们按照本文抄参考的博客的叫法,把它称为 Underlying Probabilistic Model(UPM),它的求法将在这一节解释
-
变点先验 p(rt∣rt−1):它的求法将在这一节解释
这张图说明了这个递推流程:
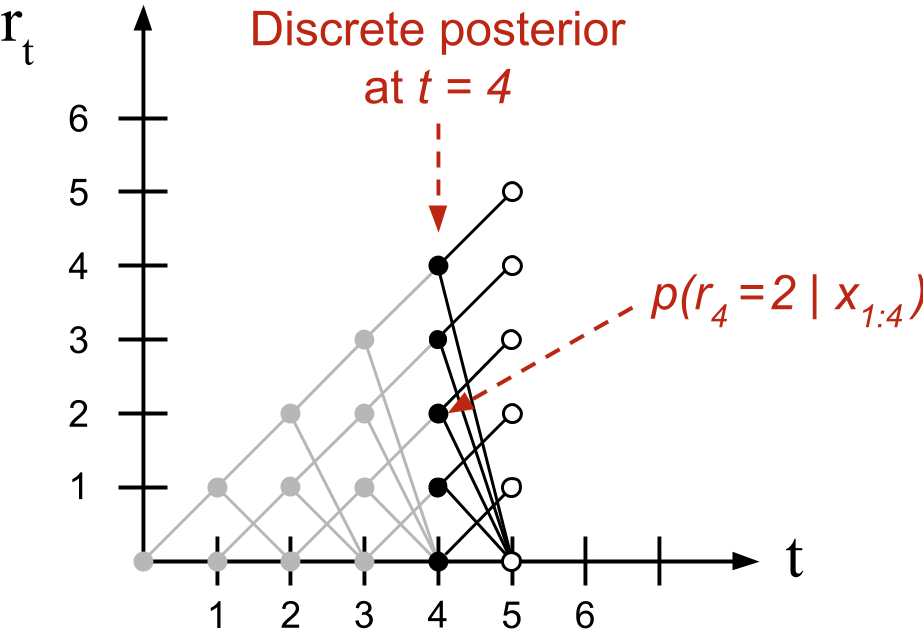
图片来源:Bayesian Online Changepoint Detection
当然,在开始这个递推流程之前,我们需要手动定义初始值 p(r0,x=∅)=p(r0),定义方式将在这一节解释。
变点先验
贝叶斯方法的特点就是能利用先验信息,所以我们可以把我们对变点的先验估计通过 hazard function 塞进模型里。
我们假设:
p(rt∣rt−1)=⎩⎨⎧H(rt−1+1)1−H(rt−1+1)0if rt=0if rt=rt−1+1otherwise
H(τ) 是 hazard function,描述的是个体在 τ 时刻死亡的概率(…)。当然“死亡”这个词可以换成别的什么特殊事件,比如在这里 H(τ) 描述的就是在 run length =τ 时(在这之前都没出现变点)出现变点的概率。
Survival Function
设 T≥0 是一个表示当前 run length 长度的随机变量。S(τ) 是 survival function,表示 run length 超过 τ 的概率:
S(τ)=P(T≥τ)=1−F(τ)=τ′=τ∑∞f(τ′)
其中 F(τ)=P(T<τ)。f(τ) 表示当前 run length =τ 的概率,是一个概率密度函数。可以看到有:
f(τ)=F′(τ)=−dτdS(τ)
Hazard Function
那么由 hazard function 的定义:
H(τ)=Δτ→0limΔτp(τ≤T<τ+Δτ∣T≥τ)=Δτ→0limp(T≥τ)Δτp(τ≤T<τ+Δτ)=S(τ)f(τ)
这里 f(τ) 是我们自己定的一个先验。
当 f(τ) 正好被定为一个指数分布(或几何分布(离散))时:
f(τ)=λe−λτ
F(τ)=1−e−λτ
S(τ)=1−F(τ)=e−λτ
此时 H(τ)=S(τ)f(τ)=λ 是一个常数(但论文里面写的是 λ1,我也不知道我哪里推错了…)。
递推初始值
我们需要给 p(r0) 赋一个初始值,分为两种情况:
- 第一个观测到的数据点之前(t=0)就是一个变点。论文中给的例子是对游戏数据序列建模,游戏开始的时刻一定是个变点。那么显然有:
p(r0=0)=1
但这个假设并不总是成立。
- 假设我们现在有最近一段时间的历史数据,并且我们认为第一个变点会在未来某个时刻出现。论文给的例子是对气象数据建模。这时初始值为归一化后的 survival function:
p(r0=τ)=Z1τ′=τ+1∑∞f(τ′)
其中 Z 是一个归一化常数。
UPM
好的那么现在 p(xt+1∣rt,xt(r)) 就是最后一个要算的东西了,我们把它写成边缘分布:
p(xt+1∣rt,xt(r))=∫EF modelp(xt+1∣η)EF posteriorp(ηt(r)=η∣rt,xt(r))dη
ηt(r) 表示在 t 时刻 run length =r 时的超参数,第一项的意义是 x 服从参数为 η 的指数族分布(Exponential Family),然后对这个指数族分布建模。第二项是 η 的后验。
η 的后验并不好计算,而且这里还要对每个 η 求积分,也不好算。所以我们往往希望 η 的先验跟它的似然共轭(conjugate),使得先验与后验的形式相同,这样就能简化计算。
共轭先验
假设 X 是已经观测到的数据,x^ 是要预测的新数据点,η 是模型参数,α 是超参数。那么:
p(x^∣X,α)=∫modelp(x^∣η)posteriorp(η∣X,α)dη
这里 η 的先验跟它的似然是共轭的,所以 η 的后验跟它的先验的形式相同,只是超参数不同:
p(η∣X,α)=p(η∣α′)
那么有:
p(x^∣X,α)=∫p(x^∣η)p(η∣X,α)dη=∫p(x^∣η)p(η∣α′)dη=p(x^∣α′)
也就是说 x^ 的后验跟它的先验的形式也是相同的。如果我们能算出 η 的后验的超参数 α′,就能在不直接算后验 p(η∣X,α) 也不算积分的情况下直接算出 p(x^∣X,α)。
而当 η 的似然是指数族分布时,就一定能写出其共轭先验分布,且后验的超参数 α′ 能够很轻松的求出来。
指数族分布
指数族是一类分布,包括高斯分布、伯努利分布、二项分布、泊松分布、Beta 分布、Dirichlet 分布、Gamma 分布等一系列分布。指数族分布可以写为统一的形式:
p(x∣η)=h(x)exp(η⊤U(x)−A(η))=exp(A(η))1h(x)exp(η⊤U(x))=g(η)h(x)exp(η⊤U(x))
其中,h(x) 是 underlying measure(没找到啥合适的翻译);U(x) 是充分统计量(sufficient statistic),包含样本集合的所有信息,如高斯分布中的均值 μ 和方差 σ;g(η)=exp(A(η))1 是正则函数(normalizer);A(η) 是对数正则函数(log normalizer),用于保证:
exp(A(η))1∫h(x)exp(η⊤U(x))dx=1
A(η) 叫 log normalizer 这个名字是因为由上式可以推出:
A(η)=log∫h(x)exp(η⊤U(x))dx
跟似然 p(x∣η) 共轭的 η 的先验为:
p(η∣χ,ν)=f(χ,ν)g(η)νexp(η⊤χ)
其中 χ,ν 是超参数,f(χ,ν) 取决于指数族分布的具体形式。
由贝叶斯公式,后验正比于似然 × 先验,所以:
p(η∣X,χ,ν)∝p(X∣η)p(η∣χ,ν)∝似然((i=1∏Nh(xn))g(η)Nexp(η⊤n=1∑Nu(xn)))先验(f(χ,ν)g(η)νexp(η⊤χ))∝(i=1∏Nh(xn))f(χ,ν)g(η)N+νexp(η⊤n=1∑Nu(xn)+η⊤χ)∝g(η)N+νexp(η⊤n=1∑Nu(xn)+η⊤χ)
最后一步是因为 (∏i=1Nh(xn))f(χ,ν) 是跟 η 无关的,所以可以去掉。
可以看到后验 p(η∣X,χ,ν) 跟先验 p(η∣χ,ν) 的形式是一样的,只是超参数上有区别:
ν′=νprior+N
χ′=χprior+n=1∑Nu(xn)
所以如果似然是指数族分布,那么在先验的超参数上加一个项就可以得到后验的超参数,是种很简便的方法。
又一个递推
现在 p(xt+1∣rt,xt(r)) 可以被表示成 p(xt+1∣νt(r),χt(r)),相当于我们的目标变成了求 νt(r) 和 χt(r),而且要对每一个可能的 rt=r≤t(即 X=xt(r)=x(t−r):t)都算一个 νt(r) 和 χt(r):
νt(r)=νt−1(r−1)+1
χt(r)=χt−1(r−1)+u(xt)
νt0=νprior
χt0=χprior
这个递推的过程大概是这样:
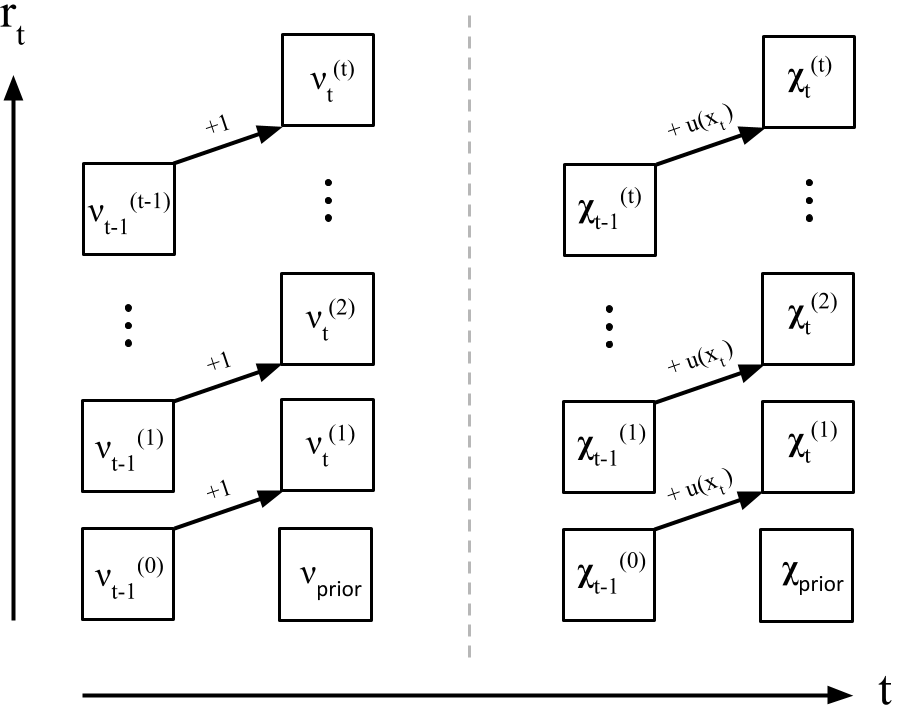
图片来源:Bayesian Online Changepoint Detection
完整算法
有空再说,我先摸下 🐟…
参考



