TIP
Radford Neal: I don’t necessarily think that the Bayesian method is the best thing to do in all cases..
Geoff Hinton: Sorry Radford, my prior probability for you saying this is zero, so I couldn’t hear what you said.
关于贝叶斯估计
X 的概率密度函数为 pθ(X),现在观测到了一组样本 (X1,X2,…,Xn)=(x1,x2,…,xn),要估计参数 θ。
极大似然估计
极大似然估计(Maximum Likelihood Estimation,MLE),频率学派的思想。频率学派的观点是:模型参数 θ 存在唯一真值,只是这个真值是未知的。如果当 θ=θ^MLE 时,事件 (X1,X2,…,Xn)=(x1,x2,…,xn) 发生的可能性最大,那么就说 θ^MLE 是 θ 的极大似然估计。
θ^MLE=argθmaxpθ(x)=argθmaxi=1∏npθ(xi)=argθmaxlogi=1∏npθ(xi)=argθmaxi=1∑nlogpθ(xi)=argθmin−i=1∑nlogpθ(xi)
也就是说最后需要优化的是 Negative Log Likelihood (NLL)。经常看到的用频率学派的方法求抛硬币概率的问题,本质上就是在优化 NLL:
抛硬币可以看做参数为 θ 的 Bernoulli 分布:
pθ(xi)={θ1−θxi=1xi=0=θxi(1−θ)1−xi
那么 NLL:
NLL=−i=1∑nlogpθ(xi)=−i=1∑nlogθxi(1−θ)1−xi
令导数为 0 来求极值:
NLL′=−i=1∑n(θxi+(1−xi)1−θ−1)=0
⇒θ∑i=1nxi−1−θn−∑i=1nxi=0
⇒θ=n∑i=1nxi
即 θ 为正面的次数除以总共的抛硬币次数。
贝叶斯估计
贝叶斯估计(Bayesian Estimation),贝叶斯学派的思想。贝叶斯学派认为 θ 也是随机的,和一般的随机变量没有本质区别,因此只能根据观测样本去估计参数 θ 的分布。其基础是贝叶斯公式:
p(θ∣x)=p(x)p(x∣θ)p(θ)
p(x)=θ∑p(x∣θ)p(θ)
θ^BE=E[p(θ∣x)]
其中:
- p(θ):先验(prior),指在没有观测到任何数据时对 θ 的预先判断,比如认为硬币大概率是均匀的,所以 θ 的先验可以是最大值取在 0.5 处的 Beta 分布;
- p(x∣θ):似然(likelihood),假设 θ 已知后,观测数据应该是什么样子;
- p(θ∣x):后验(posterior),最终的参数分布;
- p(x),样本的先验,一个常量(和要估计的参数无关)。
相当于贝叶斯估计是在 θ 服从先验分布 p(θ) 的前提下,然后根据观测到的样本去校正先验分布,最终得到后验分布 p(θ∣x),然后取后验分布的期望作为参数的估计值。
如果先验是均匀分布,则贝叶斯估计等价于极大似然,因为先验是均匀分布相当于对参数没有任何预判。
最大后验估计
贝叶斯估计估计的是 θ 的后验分布,而最大后验估计(Maximum a Posteriori,MAP)考虑的是后验分布极大化时 θ 的取值:
θ^MAP=argθmaxp(θ∣x)=argθmin−logp(θ∣x)=argθmin−logp(x)p(x∣θ)p(θ)=argθmin−logp(x∣θ)−logp(θ)+logp(x)=argθmin−logp(x∣θ)−logp(θ)
−logp(x∣θ) 就是 NLL,所以相比 MLE,MAP 就是在优化时多了一个先验项 p(θ)。在有的情况下,−logp(θ) 可以看做用 MLE 时结构化风险里的正则化项,比如当先验是一个高斯分布:
p(θ)=constant×e−2σ2θ2
constant 是一个参数无关的常数项,在上式中它相当于 2πσ1。那么:
−logp(θ)=constant+2σ2θ2
这时的 −logp(θ) 就相当于一个 L2 正则化项(倾向于取小值)。
而当先验是一个拉普拉斯分布(Laplace Distribution)时,−logp(θ) 相当于一个 L1 正则化(倾向于取 0 使权重稀疏)。
MAP 提供了一个直观的方法来设计复杂但可解释的正则化项,比如可以通过把混合高斯分布作为先验来得到更复杂的正则化项。
贝叶斯神经网络
这一节主要基于论文:
Weight Uncertainty in Neural Networks. Charles Blundell, et al. ICML 2015. [Paper]
在看这一节之前,或许先去看看概率图模型中的贝叶斯网络部分比较好。
优点:
神经网络模型
这是一个神经元:
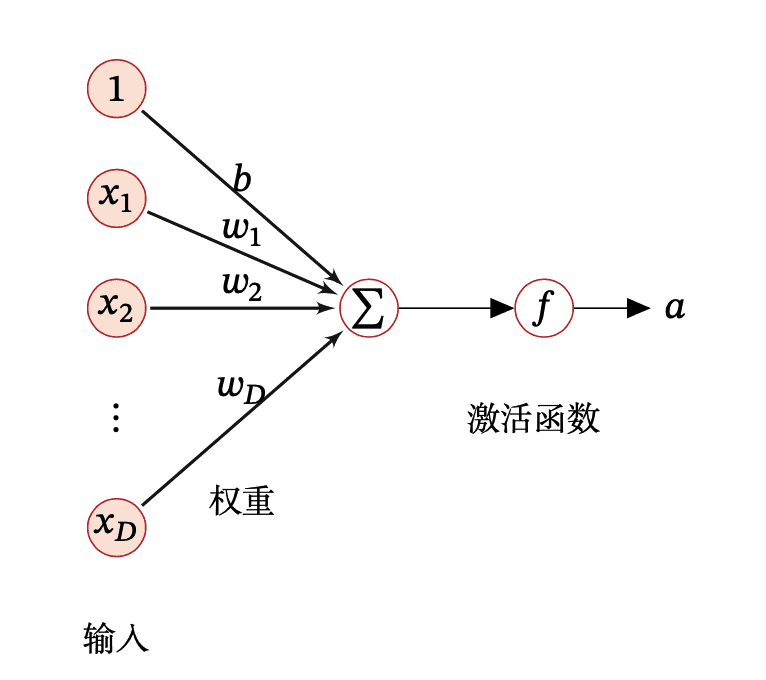
一般的神经网络中,w 和 b 都是确定的值。对于数据集 D={(x1,y1),…,(xn,yn)},其学习可以视作是一个极大似然估计:
wMLE=argwmaxlogp(D∣w)=argwmaxi=1∑nlogp(yi∣xi,w)
有些时候我们对 w 有一些偏好,于是如之前所说,引入先验(最大后验估计)可以引入正则化项:
wMAP=argwmaxlogp(w∣D)=argwmaxlogp(D∣w)+logp(w)
气氛突然贝叶斯了起来
而在贝叶斯神经网络(Bayesian Neural Network,BNN)中,w 和 b 由确定的值变为了分布,因此概率模型就变为了:
p(y∣x)=Ep(w∣D)[p(y∣x,w)]
那么存在两个问题:
-
后验 p(w∣D) 是 intractable 的。由贝叶斯公式:
p(w∣D)=p(D)p(D∣w)p(w)
而输入数据分布 p(D) 通常是是 intractable 的,因为这相当于要对所有可能的 w 求和(或积分):
p(D)=w∑p(D∣w)p(w)
-
期望 p(y∣x) 也不好求,因为这相当于要对每一个可能的 p(w∣D) 计算神经网络的预测值
朋友,搞不定的分布就上变分推断,乌拉!(不是
变分推断
对于第一个问题求后验 p(w∣D),可以用变分推断(variational inference)来解决。变分推断可以参考这里,其思想是用一个由参数 θ 控制的分布 q(w∣θ) 来近似 p(w∣D),这两个分布之间的 KL 散度要尽可能小:
θ*=argθminKL[q(w∣θ)∥p(w∣D)]=argθminw∑q(w∣θ)logp(w∣D)q(w∣θ)=argθminw∑q(w∣θ)logp(D∣w)p(w)q(w∣θ)p(D)=argθminw∑q(w∣θ)logp(w)q(w∣θ)−w∑q(w∣θ)logp(D∣w)+w∑q(w∣θ)logp(D)=argθminKL[q(w∣θ)∥p(w)]−Eq(w∣θ)[logp(D∣w)]
写成目标函数就是:
F(D,θ)=complexity costKL[q(w∣θ)∥p(w)]−likelihood costEq(w∣θ)[logp(D∣w)](1)
这个函数也被称为 variational free energy,就是 ELBO 加个负号。所以我们要最大化 ELBO,但要最小化 variational free energy。
式 (1) 可以被看做两种代价的组合:
相当于既要尽可能拟合样本,又要尽可能符合先验,在两种代价中取平衡,是一个 trade-off 的过程,可以看做正则化。
式 (1) 是个优化问题,所以可以上梯度下降。但在这之前,还有一些问题需要解决,因为式 (1) 没法求梯度。
蒙特卡洛采样
式 (1) 的第一项中,q(w∣θ) 是个我们自己定的分布(通常是高斯分布),p(w) 是个我们自己定的先验(通常也是高斯分布),都有闭式解,可以直接对 θ 求梯度。
主要问题在第二项 Eq(w∣θ)[logp(D∣w)] 上。这是个期望,它不好求,那么算它的时候一般会喜闻乐见地用蒙特卡洛采样来近似,即根据 q(w∣θ) 采样 M 个 wi,然后有:
Eq(w∣θ)[logp(D∣w)]≈M1i=1∑Mlogp(D∣wi)
于是近似之后这一项就变得跟参数 θ 无关了,梯度下降时这一项关于 θ 的梯度会为 0。这是因为 z 和 θ 之间不是确定性函数关系,而是一种采样的关系。于是就有一种叫重参数化的 trick,把这种采样的关系转变成确定性函数关系。
重参数化
重参数化(reparameterization)是变分自编码器(Variational Auto-Encoder, VAE)引入的操作。先引入一个分布为 p(ϵ) 的随机变量 ϵ,然后把期望 Eq(w∣θ)[logp(D∣w)] 重写为:
Eq(w∣θ)[logp(D∣w)]=Ep(ϵ)[logp(D∣t(θ,ϵ))]
其中 w≜t(θ,ϵ),是一个确定性函数,这样就可以先从 p(ϵ) 中采样出 ϵ,然后可导地引入 w。例如 q(w∣θ)=N(μ,σ2),μ,σ 依赖于参数 θ,那么可以把 w 写为:
w≜t(θ,ϵ)=μ+σ⊙ϵ
其中 ϵ∼N(0,1)。
而该论文对此作了推广。对于期望 Eq(w∣θ)[logp(D∣w)],它的梯度 ∂θ∂Eq(w∣θ)[logp(D∣w)] 不好直接算,采样之后梯度又为 0,那么能不能把求导移到期望里面去:Eq(w∣θ)[∂θ∂logp(D∣w)]?
并不能,因为期望(积分)是跟参数 θ 有关的,而 logp(D∣w) 是与 θ 无关的,把求导移进去的话梯度又为 0 了。因此该论文把 w 写为 t(θ,ϵ),其中 ϵ∼q(ϵ)。然后它证明了对于函数 f(w,θ),只要有 q(ϵ)dϵ=q(w∣θ)dw,就有:
∂θ∂Eq(w∣θ)[f(w,θ)]=∂θ∂∫f(w,θ)q(w∣θ)dw=∂θ∂∫f(w,θ)q(ϵ)dϵ=Eq(ϵ)[∂w∂f(w,θ)∂θ∂w+∂θ∂f(w,θ)]
这时就可以把求导移进期望里了。从直觉上来理解的话,现在 Eq(w∣θ)[logp(D∣w)] 可以写成:
Eq(w∣θ)[logp(D∣w)]=Eq(ϵ)[logp(D∣t(θ,ϵ))]
那么现在期望就和 θ 无关,而似然则和 θ 有关了,于是就可以把求导移进去了。
论文里令 f(w∣θ)=logq(w∣θ)−logp(w)p(D∣w),则:
F(D,θ)=Eq(w∣θ)[f(w∣θ)]≈i=1∑nlogq(wi∣θ)−logp(wi)−logp(D∣wi)
这个近似把 KL 散度也蒙特卡洛了,这种做法摆脱了对 KL 散度有闭式解的要求。虽然在很多情况下 KL 散度能写出闭式解,但这样可以适配更多的先验后验分布形式。
梯度下降
为了计算方便,论文用了平均场近似(mean-field approximation)。即令变分后验 q(w∣θ) 为一个平均场分布族,即认为各个参数 wi 之间相互独立,每个参数 wi 都服从高斯分布(也即协方差矩阵除了对角线以外都为 0,所以原文用的是 diagonal Gaussian distribution 这个词),那么有:
q(w∣θ)=i∏qi(wi∣θ)=i∏N(wi∣μi,σi2)
按照之前说的重参数化操作,wi 可以写为:
wi=μi+σi⊙ϵi
ϵi∼N(0,1)
然后令 f(w∣θ)=logq(w∣θ)−logp(w)−p(D∣w)。因为最大化 p(D∣w) 跟最小化 L(w) 是一回事,所以也可以写成 f(w∣θ)=logq(w∣θ)−logp(w)+L(w)。
而 θ=(μ,σ),那么分别对 μ 和 σ 求梯度:
Δμ=∂w∂f(w,θ)+∂μ∂f(w,θ)
Δσ=∂w∂f(w,θ)⋅ϵ+∂σ∂f(w,θ)
为了保证 σ 非负,论文又把 σ 写成了 σ=log(1+exp(ρ)),所以现在变成了 θ=(μ,ρ),关于 ρ 的梯度为:
Δρ=∂w∂f(w,θ)1+exp(−ρ)ϵ+∂ρ∂f(w,θ)
然后按梯度下降更新 μ,ρ 即可:
μ←μ−αΔμ
ρ←ρ−αΔρ
胡思乱想
0x00
打算理 BNN 是因为看到了一篇论文:
Uncertainty-guided Ccontinual Learning with Bayesian Neural Networks. Sayna Ebrahimi, et al. ICLR 2020. [Paper] [Code]
个人觉得它的思想非常简洁,就是对 BNN 参数更新的学习率 α 做了修改,以至于让我这种菜鸡都能立马理解,甚至觉得我要是早点入这个坑我也能想出这个 idea(不是没有我没这样说过
方差 σi 可以被看做参数 wi 的不确定度(uncertainty),方差越大说明这个参数对当前任务越重要,那么在后面的任务中它的更新幅度就应该小一点,反之则应该大一点。也就是说参数重要性 Ω 被定义为:
Ωi∝σi1
而与一般的 regularization-based continual learning 方法加正则项的做法不同,这篇论文直接通过控制学习率来控制更新幅度,不过它只更新了 μ 的学习率,ρ 的学习率则一直保持不变:
αiμ←Ωiαiμ
0x01
贝叶斯神经网络是一种深度学习方法,诞生在一个 Autograd 工具大行其道的时代,因此对于最小化 Eq(w∣θ)[f(w,θ)] 这个优化问题,它可以直接上梯度下降。
还有一种贝叶斯系方法叫 ADF(Assumed Density Filtering),或者叫它在线变分贝叶斯(Online Variational Bayes)可能还更容易理解一点。在第 n 个数据集 Dn 上估计参数时,它会把 f(w,θ) 中的参数先验 pn(w) 替换为上一个数据集上的参数后验 pn−1(w∣Dn−1)=qn−1(w)。
在 ADF 诞生的那个年代,深度学习还是个冷门领域,也并没有什么 Autograd 工具能给你用。因此 ADF 在求极小值时直接用了“使导数为 0”这种硬核方法:
∂θ∂Eq(w∣θ)[f(w,θ)]=Eq(ϵ)[∂w∂f(w,θ)∂θ∂w+∂θ∂f(w,θ)]=0
因为 q 是指数族分布,所以上式是有闭式解的,只是推导过程比较复杂,感兴趣的话可以看看这篇文章。之所以提到这个,是因为下面这篇论文就是套的 ADF 框架,并直接通过闭式解来更新参数:
Task Agnostic Continual Learning Using Online Variational Bayes. Chen Zeno, et al. arXiv 2018. [Paper] [Code]
而用贝叶斯性来做 continual learning 的开山之作 VCL 跟上面那篇论文的主要不同点在于,VCL 在更新参数时用了梯度下降,相当于在套 ADF 框架的同时又利用了 Autograd 的好处:
Variational Continual Learning. Cuong V. Nguyen, et al. ICLR 2018. [Paper] [Code]
当然 VCL 还采样了一部分旧数据作为 coreset,coreset 也会被用于当前任务的训练,这种喜闻乐见的方法可以提高效果。
然后有空的话我或许会理一理 ADF…
参考
