Meta Learning:一种套娃算法
Aug 5, 2020 · 15 min · meta learning , deep learning
continual learning 方向 19 年之后的几篇论文搞出了一个套 meta learning 框架(主要是 MAML 这种 optimization-based 的方法)的新思路。这个思路又可以水不少论文还是很自然的,毕竟 meta learning『快速适应新任务』的思想可以看做 continual learning 的两个目标之一(学习新任务)的升级版,那么就只需要解决剩下那个目标(灾难性遗忘)就可以了。
于是这里我决定稍微理一理背后的思想是套娃 learning to learn 的 meta learning 的基本概念。
这是一篇讲 meta learning 讲得非常清楚的文章,本文很大程度上抄参考了这篇文章:
Learning to Learn Fast (Lilian Weng) [英文原版] [中文翻译]
这作者还写过一篇在 reinforcement learning 任务里面用 meta learning 的文章:
Meta Reinforcement Learning (Lilian Weng)
这是自用的对 meta learning 相关文献的记录:Literatures of Meta Learning
动机
传统监督学习的流程是,对于一个训练集 ,试图学习出一个模型 ( 是从训练数据中估计出的模型参数,决定了 的性能 ),使得损失函数 最小。
这个思路在训练集中有大量数据的情况下是行得通的。而在很多情况下,有的数据集的数据量非常少,我们很难在上面直接训练出来一个泛化能力好的机器学习模型。
但不同的相似任务之间是有联系的。比如人类学会分类新的物体并不需要很多的样本作为支撑,人类可以做到只观看一个物体的一张或几张图片,就在之后的照片中准确地识别。这就是利用了不同任务之间的联系,基于过往的经验快速地学习。比如下面这个例子,训练数据中每个类别就三个样本,然后让你判断测试数据是哪个画家的作品:

答案是 Braque。由于每个类别的样本很少,人类能答对这个问题很大程度上是依赖过往经验,而不是从头开始学习(虽然作为神人类我觉得这个问题似乎也不简单?2333)。所以就有了这样的想法:有些不同的任务之间是有一定的联系的,所以虽然我现在要做的这个任务的数据集的数据量很少,但我有很多其它的数据集,如果模型可以先在其他数据集上学到“如何快速学习新知识”的先验知识(即 learn to learn,学习出一个会学习的模型),大概就能仅用少量的数据就学会新的概念。
这就是一个套娃的过程。
事实上我们还可以继续套更多的娃,比如 learn to learn to learn,即学习一个能够学习出会学习的模型的模型(…)。甚至还可以衍生到 learn to … to learn,最终可以实现机器学习的完全自动化。
问题定义
meta learning 可以用于解决任意一类定义好的机器学习任务,如监督学习、强化学习等。这里谈的主要是监督学习(如图像分类)。
概览
假设有一个 task 的分布,我们从这个分布中采样了许多 task 作为训练集。我们希望 meta learning 模型在这个训练集上训练后,能在这个分布中所有的 task 上都有良好的表现,即使是从来没见过的 task。每个 task 可以表示为一个数据集 ,数据集中包括输入向量 和其对应的标签 ,task 分布表示为 。那么 meta learning 的优化目标是:
可以看到,一般的学习任务中,模型会在一个 task 中通过对样本的学习以对新样本做出决策;而 meta learning 把每个样本换成了一个 task,通过对多个 task 的学习以对新的 task 进行快速的学习。
数据集 通常还会被划分为训练集 support set 和测试集 query set ,即 。相当于 meta learning 的训练阶段会模拟传统训练中的测试过程。
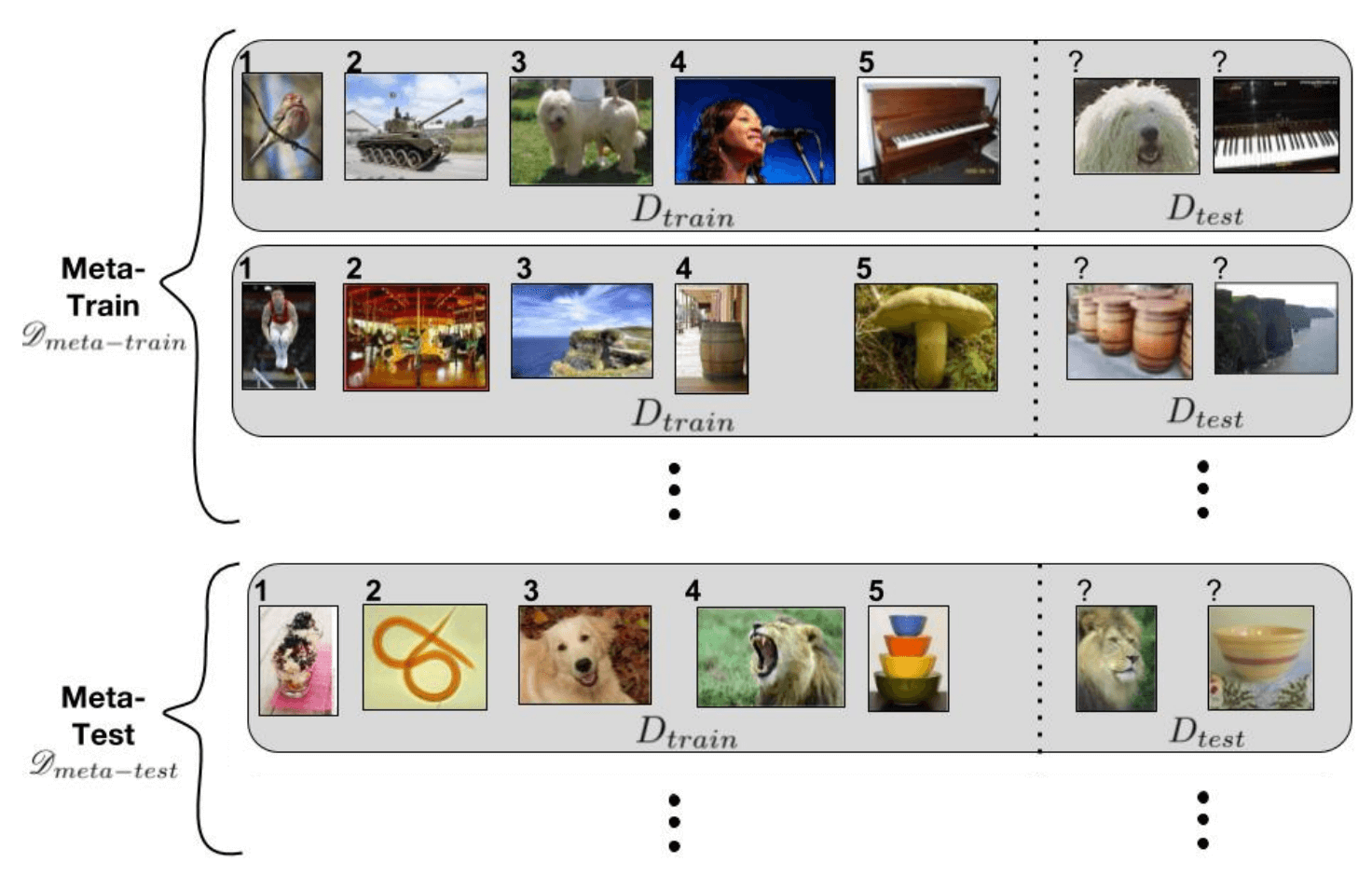
一个需要解释一下的术语是 N-way K-shot,指 support set 中有 N 类数据,每类数据有 K 个带有标注的样本。
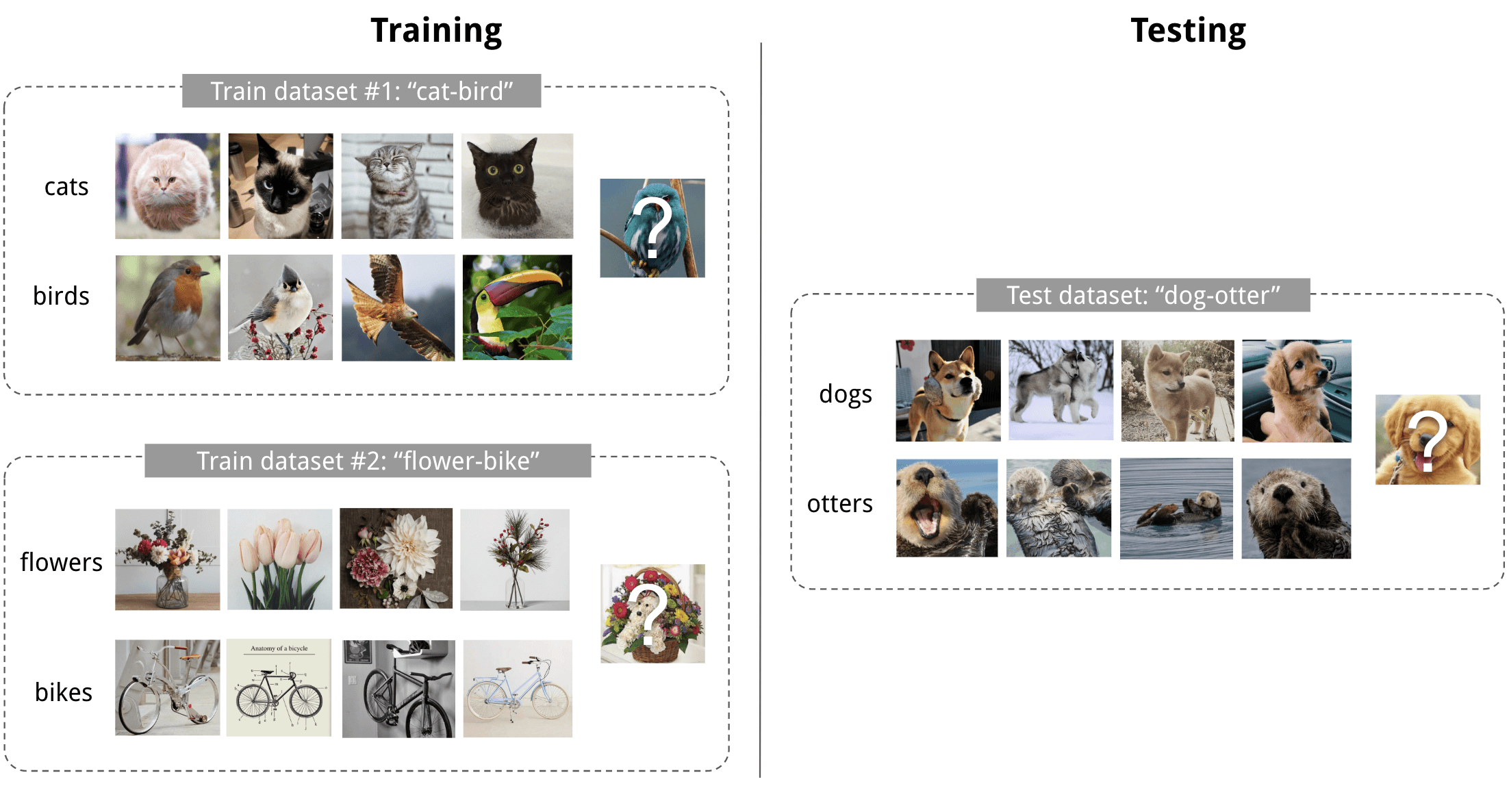
2-way 4-shot 图像分类示例。我们希望模型在知道了如何区分『猫和鸟』以及『花和自行车』后,能快速学会区分『狗和水獭』。图片来源:Meta-Learning: Learning to Learn Fast
训练过程
meta learning 的训练过程一般为,对于每一个 task :
-
采样出一个 support set 和一个 query set ;
-
在 support set 上进行学习,根据这些样本上的损失进行参数更新,得到更新后的参数 。但通常 只是一个临时参数。
这一步被叫做元学习器(meta-learner),其目的是为整个模型(学习器)该怎么更新参数提供指导;
- 用临时参数 在 query set 上计算损失,并根据这个损失来更新模型参数。这一步是永久更新,与监督学习一致。
我从直觉上来理解的话,第二步对标传统训练中的训练集上的参数更新,第三步对标测试阶段,然后用测试集上的损失来更新模型参数。通过这种方式,模型被训练出了在其他数据集上扩展的能力。
常见方法
meta learning 主要有三类常见的方法:
-
基于度量(metric-based)
思想类似于 k-NN 一类的算法。测试时会计算输入样本跟 support set 中所有样本的距离,然后根据这些距离预测标签。这种方法一般只能用于分类问题。
-
基于模型(model-based)
不对模型做任何定义,直接用另外一个神经网络把它的参数都学习出来,这个用来学习模型参数的网络一般基于 RNN。
-
基于优化(optimization-based)
相比 model-based 方法,optimization-based 方法只学习初始化参数的规则,而不学习模型架构,模型架构是提前定好的。这类方法的主要流派就是 MAML,本文后面主要会理一下 MAML。
MAML
Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks. Chelsea Finn, et al. ICML 2017. [Paper] [Code]
这是 MAML 一作:Chelsea Finn (现在是 Stanford 的 AP),她们组有不少相关的工作。
MAML(Model-Agnostic Meta-Learning)是一种通用的基于优化的算法,可以被用于任何基于梯度下降学习的模型。它的目标是学习出一组初始化参数 ,对于任意 task,这个初始化的参数都能在一步或极少步梯度下降中就快速达到最优参数解 :
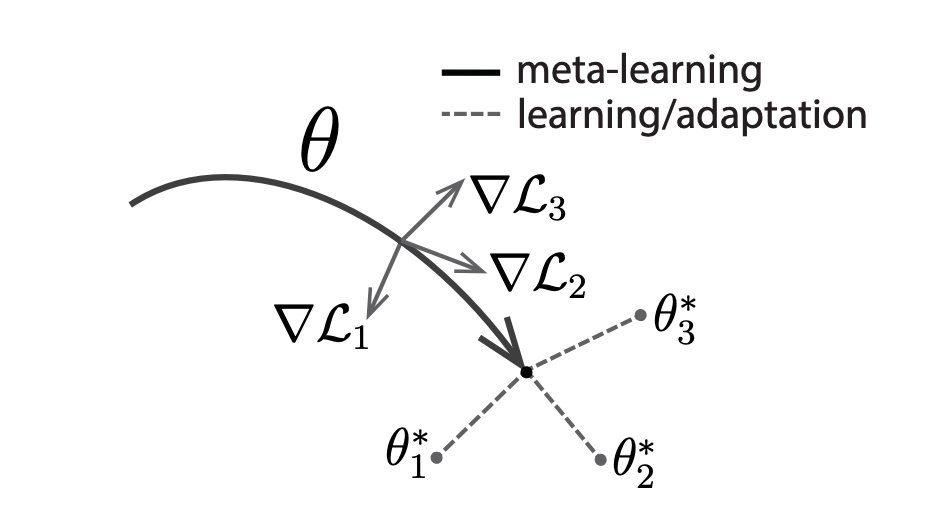
Meta-Train
MAML 的训练过程(一般被称为 meta-train)为:

可以看到对于采样出每个 task ,有两层循环:
-
inner loop:在从 task 中采样出的 support set 上计算梯度并更新参数(只更新一次),得到更新后的参数 。就像之前所说,这里的 只是一个临时参数,并不会作为最终的更新(所以实际操作上是要 copy 一份当前参数去计算 );
-
outer loop:用参数 在采样出的 query set 上计算损失,然后对参数 求梯度,然后在 上更新出最终的模型参数。
这个过程如下图所示:
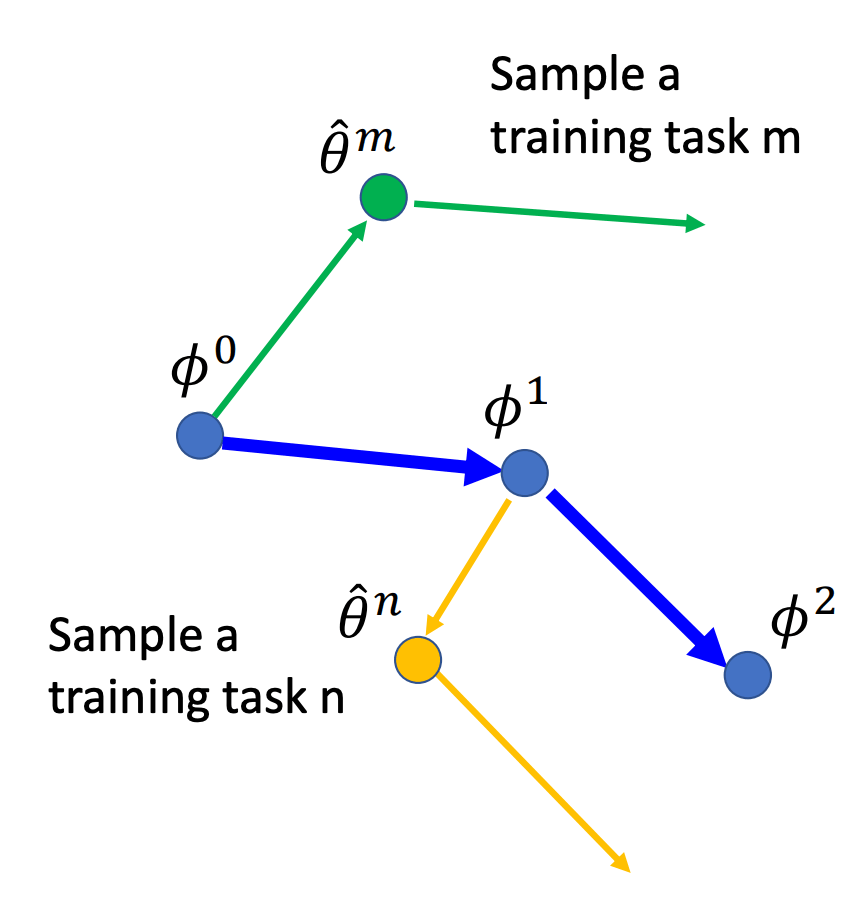
图片来源:Meta Learning,李宏毅
Meta-Test
在测试(mete-test)时,会把经过 meta-train 训练好的模型拿去测试集(新 task)的 support set 上 fine-tune,然后在 query set 上得到测试结果。fine-tune 的过程跟 meta-train 基本上差不多,不同点主要是:
-
第 1 行:meta-train 时的 是随机初始化的,而 fine-tune 时直接用了经过 meta-train 后得到的 ;
-
第 3 行:fine-tune 的时候就不存在 batch 了,只抽取一个 task 来学习;
-
第 8 行:fine-tune 的时候不存在这一步,因为这时的 query set 是用来测试模型的,不可能给你算损失然后梯度回传。所以会直接用第 6 行得到的 作为最终参数。
二阶导
outer loop 对 求导时是需要进行二阶导计算的。设模型初始参数为 ,第 次 innner loop(第 个 batch)的参数更新公式可以表示为:
那么 outer loop 中:
标红部分是二阶导。求二阶导会消耗更多的计算时间,为了节省计算成本,作者还提出了 MAML 的一阶变种 First-Order MAML(FOMAML),即直接舍弃掉二次微分项。
Transfer Learning?
MAML 的思想很像 transfer learning,即在大数据集上预训练一个模型,学习一个初始化参数,然后拿到小数据集任务上去 fine-tune。Chelsea Finn 在一篇博客中也阐述了 MAML 跟 transfer learning 的区别和联系。当某个任务的数据量过小时,把预训练模型直接拿去 fine-tune 会过拟合。因此 MAML 的核心目标是,学习一个在小数据集上更容易被 fine-tune 的初始化参数。
下图是 MAML 和一般的预训练模型的参数更新方式对比:
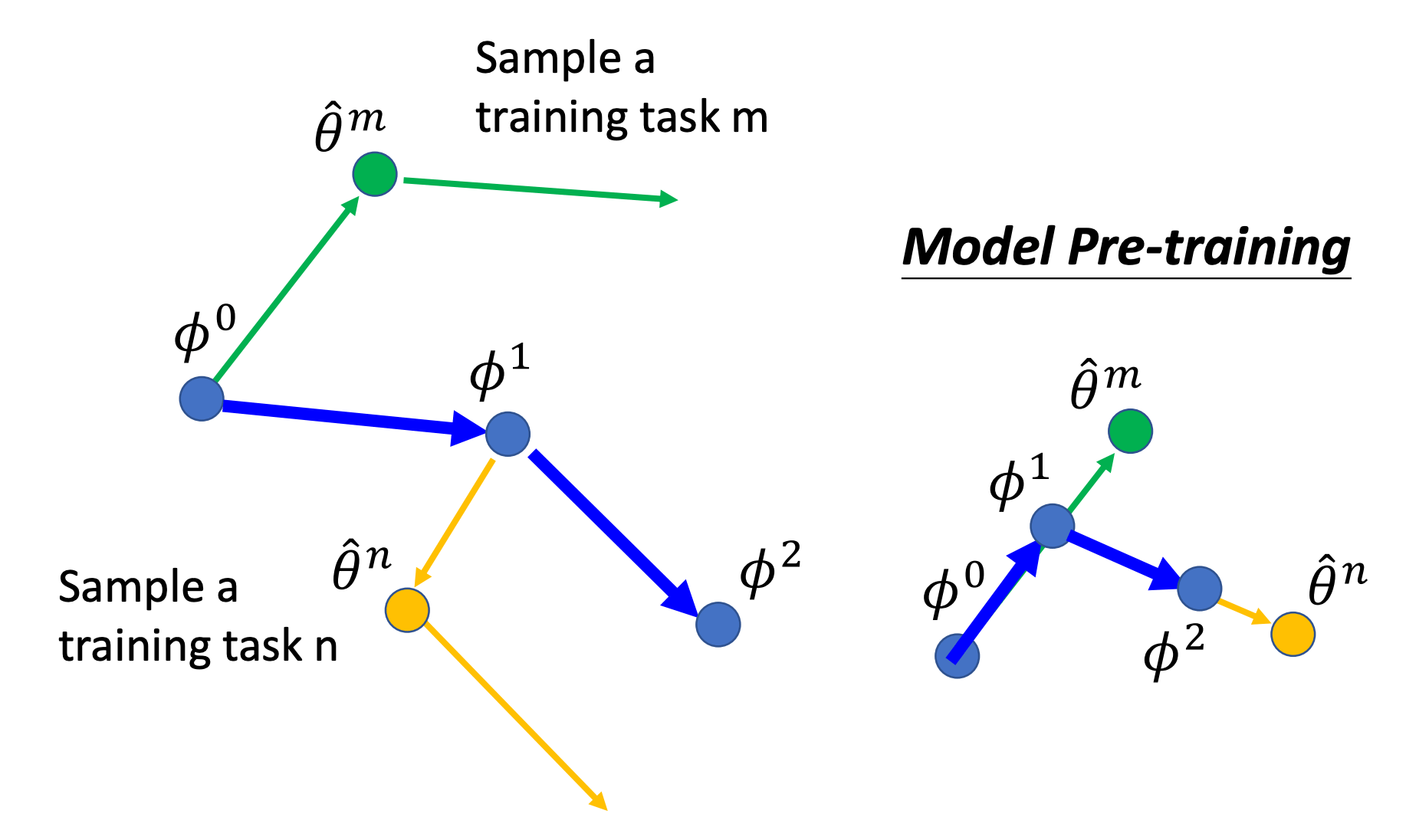
FOMAML
First-Order MAML(FOMAML),MAML 作者顺便提出的一阶版本,为了节省计算成本,直接扔掉了二次微分项。
MAML 的 outer loop 会对 而不是 求梯度,因此存在二阶梯度为:
而 FOMAML 直接对 求梯度,这样就没有二阶梯度了:
FOMAML 算法流程为:

图片来源:First-order Meta-Learned Initialization for Faster Adaptation in Deep Reinforcement Learning
从论文中的实验,包括 Reptile 论文中的实验来看,省掉二阶梯度对于结果的影响并不大。
Reptile
On First-Order Meta-Learning Algorithms. Alex Nichol, et al. arXiv 2018. [Paper] [Code] [Slide]
Reptile 是另一种一阶的 meta learning 算法,它的流程为:

带 batch 的版本就是每次采样多个 task:

Reptile 与 FOMAML 的区别在于:
-
inner loop 中会根据损失 进行 次 sgd
-
outer loop 中不再计算梯度,而是取 inner loop 更新后的参数与原模型参数的改变量的 (学习率)倍
当 时,这个算法就是 multi-task learning 用 sgd 更新一步的公式:在每个 task 上都更新一步,就相当于对所有 task 的总损失的期望求梯度然后更新了。
普通 multi-task 进行 次 sgd 求的是 ;而 Reptile 的 次 sgd 在 inner loop 里,所以它求的是 ,当 时两者是不一样的。
Reptile 的参数更新过程:
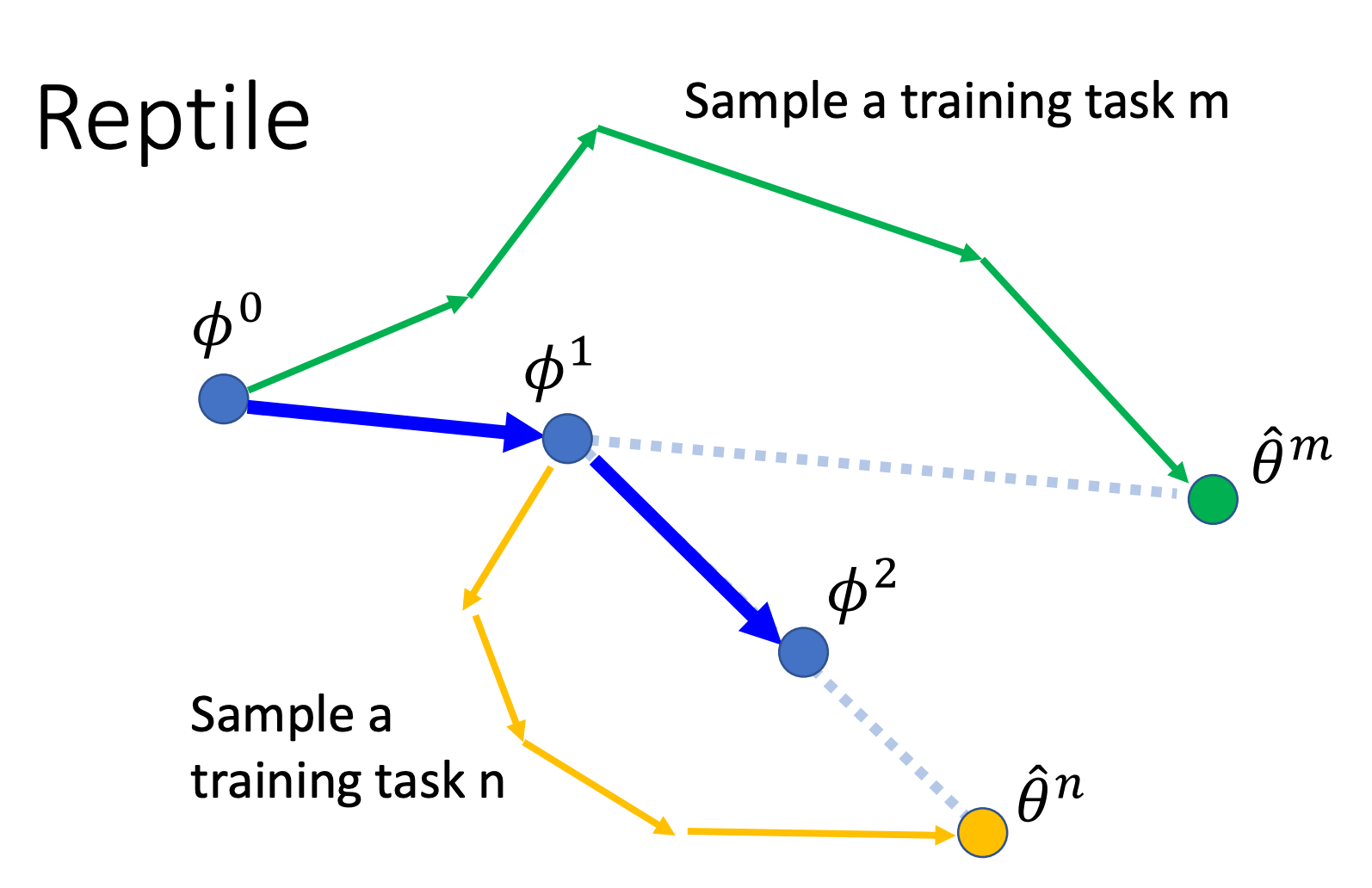
与 MAML 和 Pre-train 在一次外循环里的参数更新的对比:
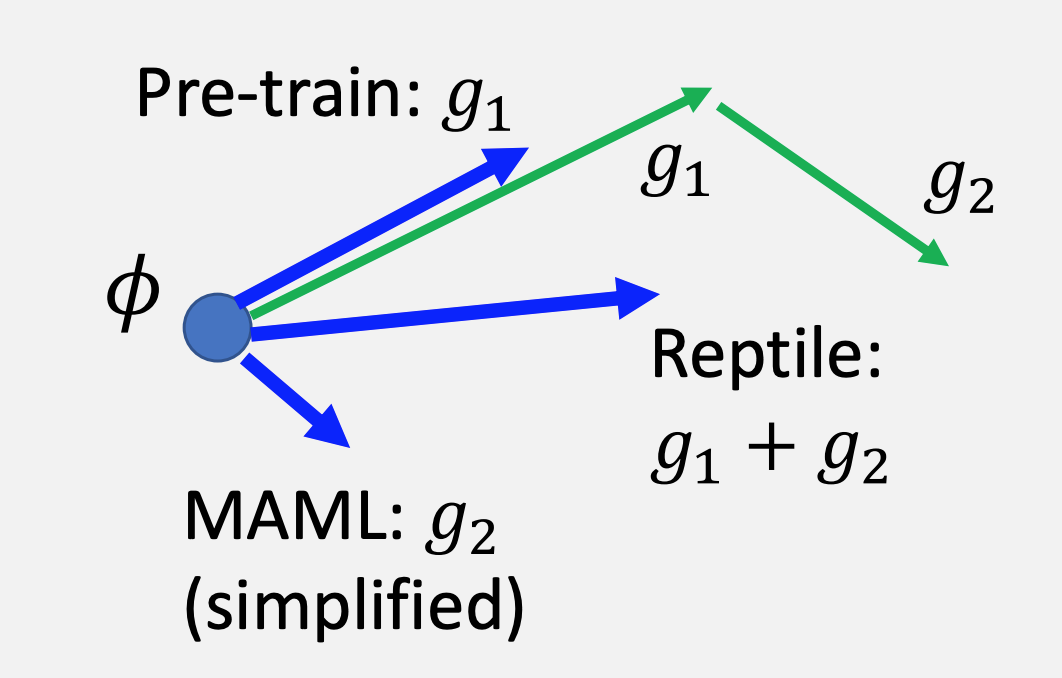
Reptile & MAML
Reptile 论文里还对 Reptile 和 MAML 的原理写了一大段分析。推了一堆公式之后,作者认为 Reptile 和 MAML 的优化目标都为(5.1 节):
-
沿 task 上的损失的平均梯度方向更新模型,使模型在当前任务上的表现更好
-
最大化同一个 task 中多个 batch 的梯度的内积。因为梯度的内积越大说明它们夹角越小,意味着它们的更新方向越相似,因此在一个 batch 上的更新同时还能提升在另外一个 batch 上的性能,从而使模型在当前任务上具有更好的泛化性。
这是一张解释第二点的图:
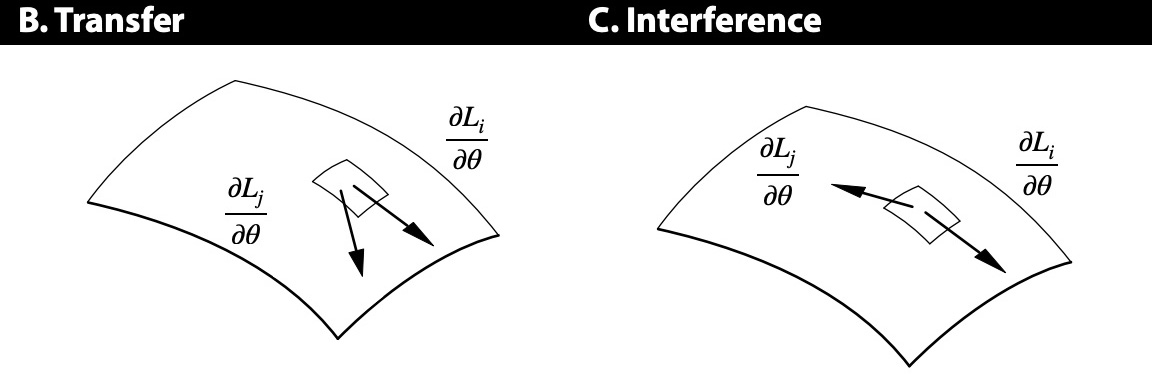
图片来源:Learning to Learn without Forgetting by Maximizing Transfer and Minimizing Interference (ICLR 2019)
参考
-
Meta Learning. Hung-yi Lee (李宏毅). [Slides: Part 1, Part 2] [Video]
-
ICML 2019 Tutorial - Meta-Learning: from Few-Shot Learning to Rapid Reinforcement Learning
-
Generalizing from Few Examples with Meta-Learning. Hugo Larochelle.
-
Learning to Learn. Chelsea Finn.
-
First-order Meta-Learned Initialization for Faster Adaptation in Deep Reinforcement Learning. Abhijat Biswas and Shubham Agrawal.