试图理一理 Transformer
Jul 17, 2020 · 9 min · deep learning
Attention Is All You Need. Ashish Vaswani, et al. NIPS 2017. [Paper] [Code]
考虑到 RNN 只能单向依次计算,所以存在以下问题:
-
时刻的计算依赖与 时刻的计算结果,限制了模型的并行能力
-
RNN 的长期依赖问题
于是这篇论文扔掉了 encoder 和 decoder 中的 RNN 结构,完全用 attention 来搞 machine translation:
-
没有 RNN 结构,所以有更好的并行能力
-
attention 机制对全局信息的处理更有效
Transformer 整体结构如下:
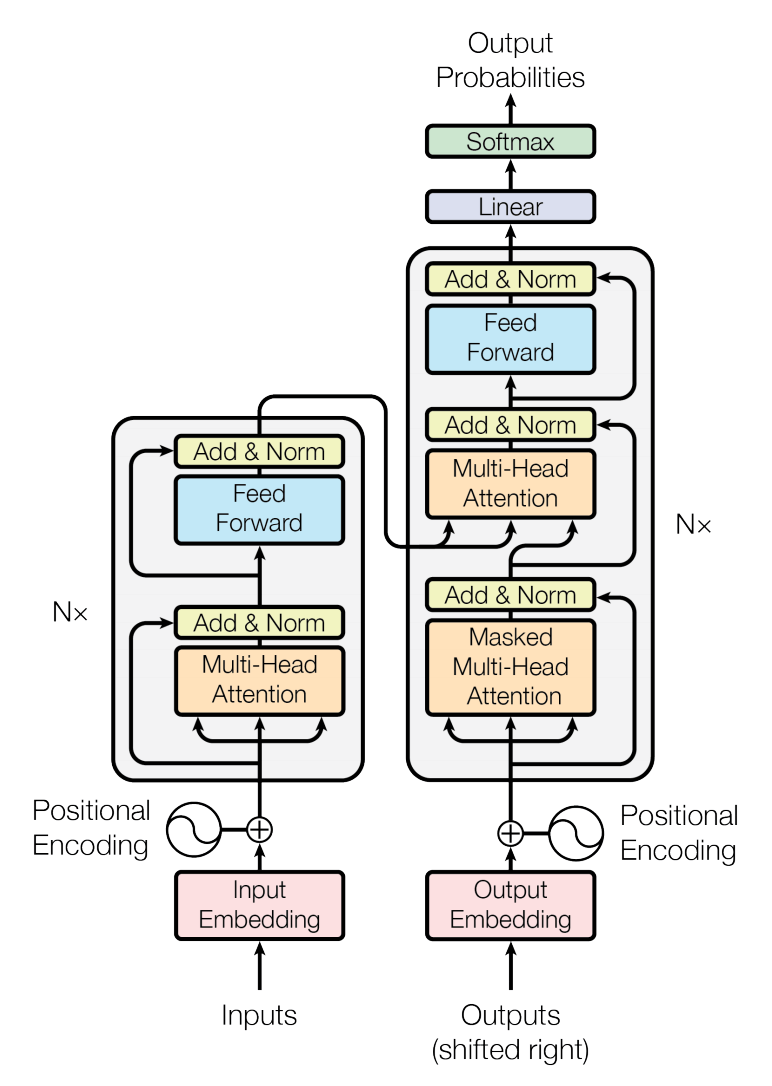
Position Embedding
Transformer 扔掉了 RNN,对输入句子的所有单词都是同时处理的,所以失去了捕捉单词的排序和位置信息的能力。如果不解决词序的问题,那即使把一句话打乱,attention 出来的结果也是一样的,相当于这就只是一个词袋模型。为了解决这个问题,论文引入 position embedding 来对单词的位置信息进行编码。最终的输入词向量 = word embedding + position embedding:
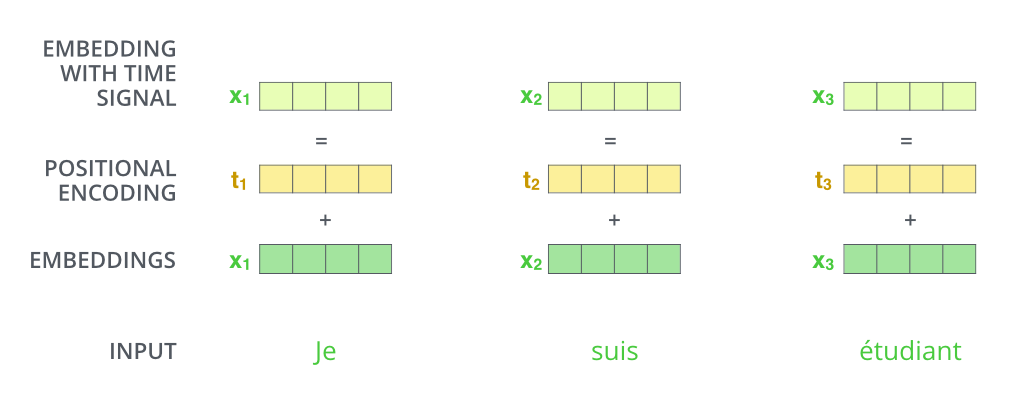
有两种搞到 position embedding 的思路:
-
学习出一份 position embedding(Convolutional Sequence to Sequence Learning. Jonas Gehring et al. ICML 2017.)
-
直接用不同频率的 sin 和 cos 函数算出来
经过实验,论文发现这俩方法效果差不多,所以选了第二种方法,因为它有以下好处:
-
不需要加额外的训练参数
-
学习出来的 position embedding 会受到训练集中序列的长度的限制,但三角函数明显不受序列长度的限制,所以能够处理训练集中没见过的序列长度
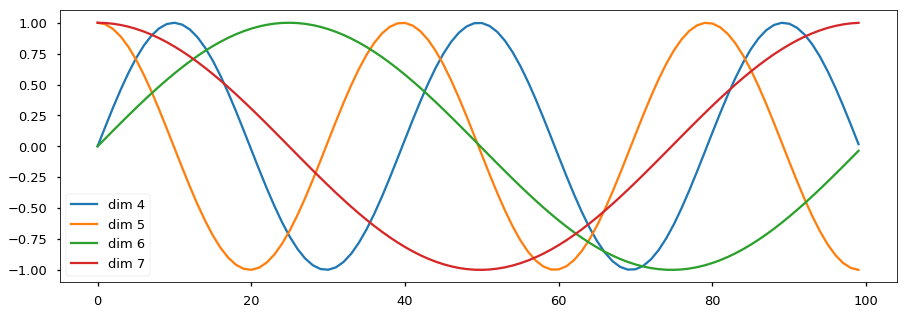
具体的位置编码公式为:
其中 为词嵌入维度(论文中为 512),pos 为该单词在序列中的位置, 为词向量的偶数维度(用第一个公式), 指词向量的奇数维度(用第二个公式)。波的频率和偏移对于每个维度是不同的:
因为三角函数还有以下特性:
所以任意位置的 都能通过 线性表达,这为模型捕捉单词之间的相对位置关系提供了非常大的便利。
Encoder
论文中的 encoder 由 N = 6 个相同的 layer 堆叠而成:
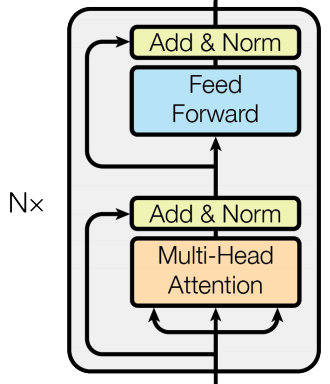
每个 layer 由两个 sub-layer 组成,分别为 multi-head self-attention 和 fully connected feed-forward network。
并且每个 sub-layer 都加了:
-
Residual Connection:解决多层神经网络训练困难的问题,通过将前一层的信息无差的传递到下一层,可以有效的仅关注差异部分
-
Layer Normalisation:对层的激活值进行归一化,可以加速模型的训练过程,使其更快的收敛 Layer Normalization. Jimmy Lei Ba, et al. arXiv 2016.
也就是输入会先进 LayerNorm,再进 sub-layer,然后加在原始输入上(虽然图上 LayerNorm 似乎在 sub-layer 后面,但代码里的确是先进 LayerNorm)。最后 6 个 layer 都跑完之后还要再单独 norm 一次(虽然图上没画但代码里写了)。
Muti-Head Self-Attention
attention 可以表示为以下形式:
其中 (value)用来求加权和得到最终的上下文向量,而 (query)和所有的 (key)会被用来计算注意力权重。如在传统的 seq2seq 结构中,它们分别由以下值经过线性变换得到:
-
:decoder 的当前输入
-
:encoder 的输出()
-
:同
而这里是 self-attention,所以 由同一个值 经过线性变换得到, 在第一个 layer 为输入的词向量序列,在之后的 layer 则为上一个 layer 的输出。
而 multi-head attention 就是通过 个不同的线性变换得到不同的 ,最后将这 个 attention 结果拼接起来:
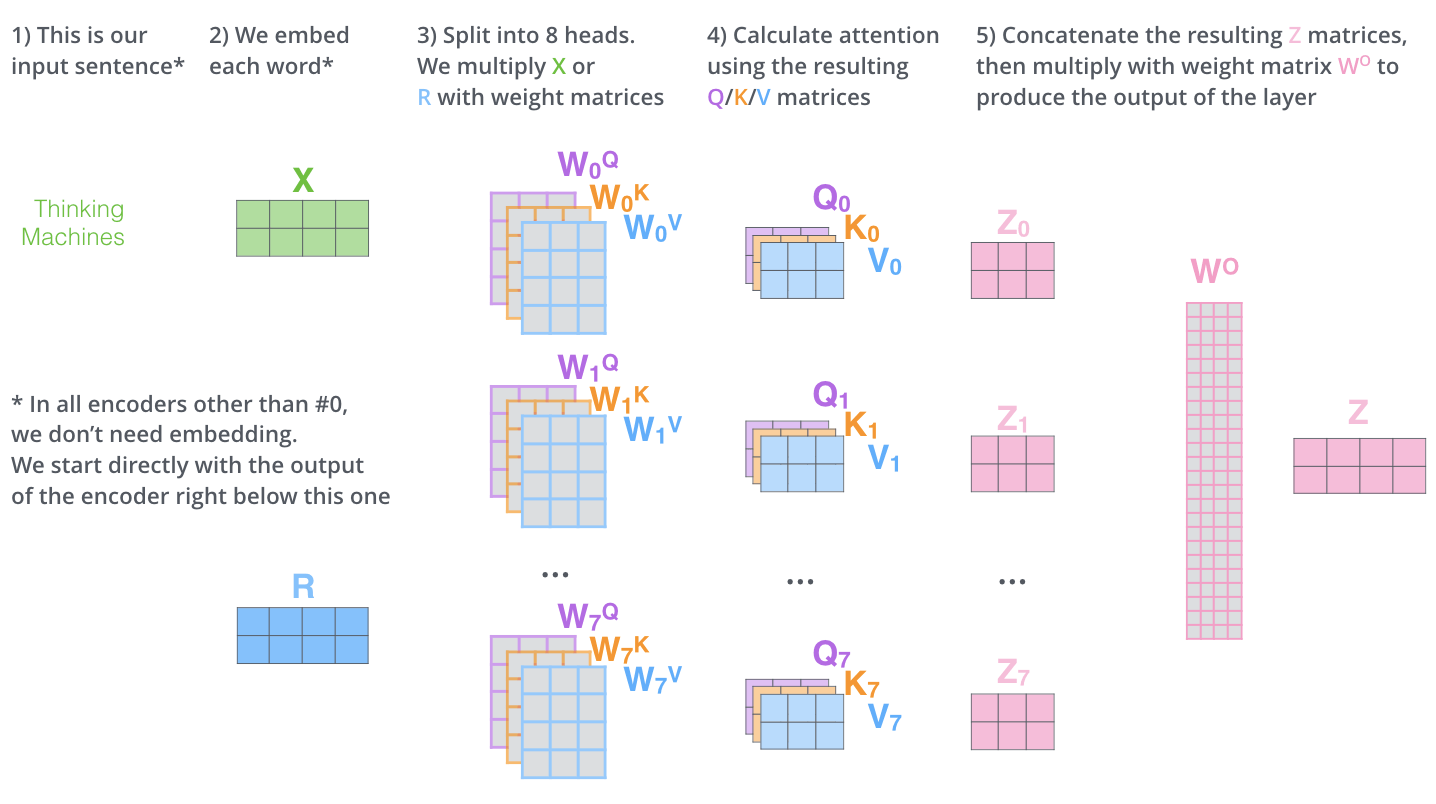
这里的 attention 计算公式为(scaled dot-product):
注意:这里跟 是矩阵相乘,不是 element-wise 相乘。
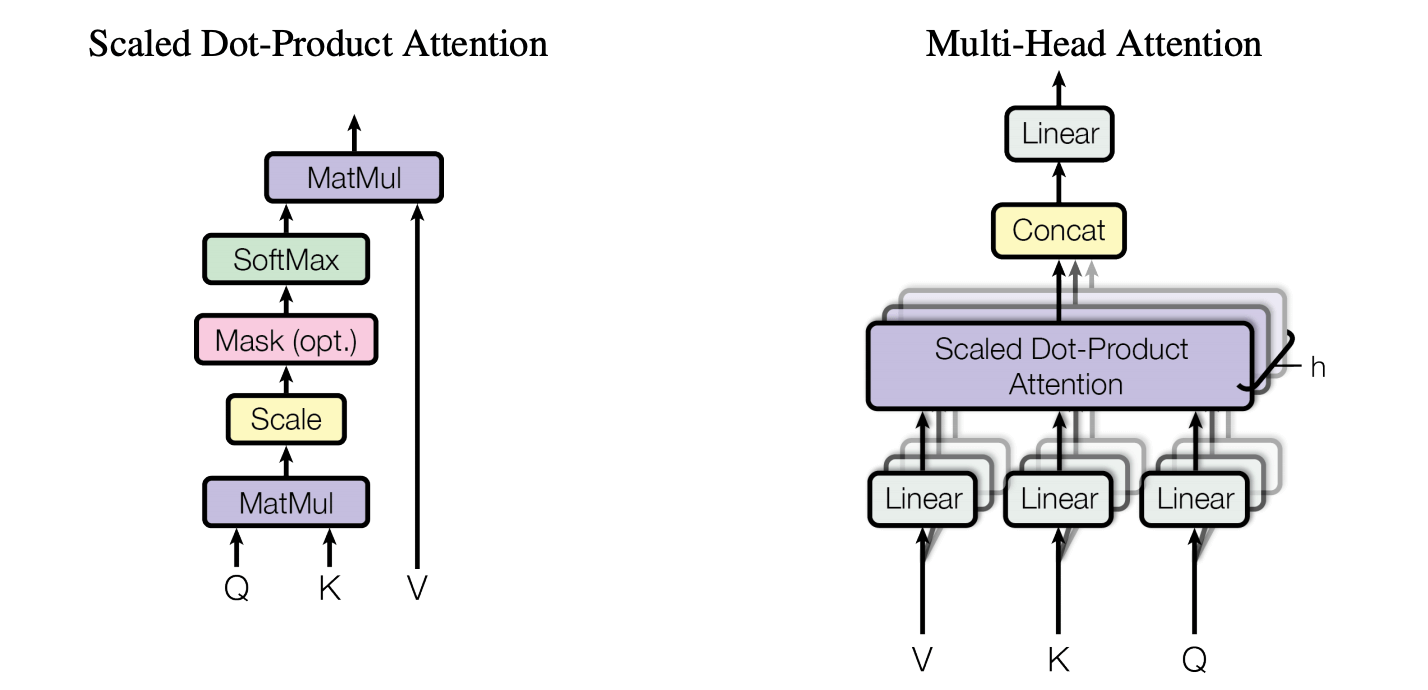
其中 。除以 是因为, 越大 就会越大,可能就会将 softmax 函数推入梯度极小的区域,所以要用 对 进行缩放。
图中的 mask 只会在 decoder 中被用到。
Feed-Forward Network
第二个 sub-layer 是一个前馈网络:
Decoder
encoder-decoder 结构:
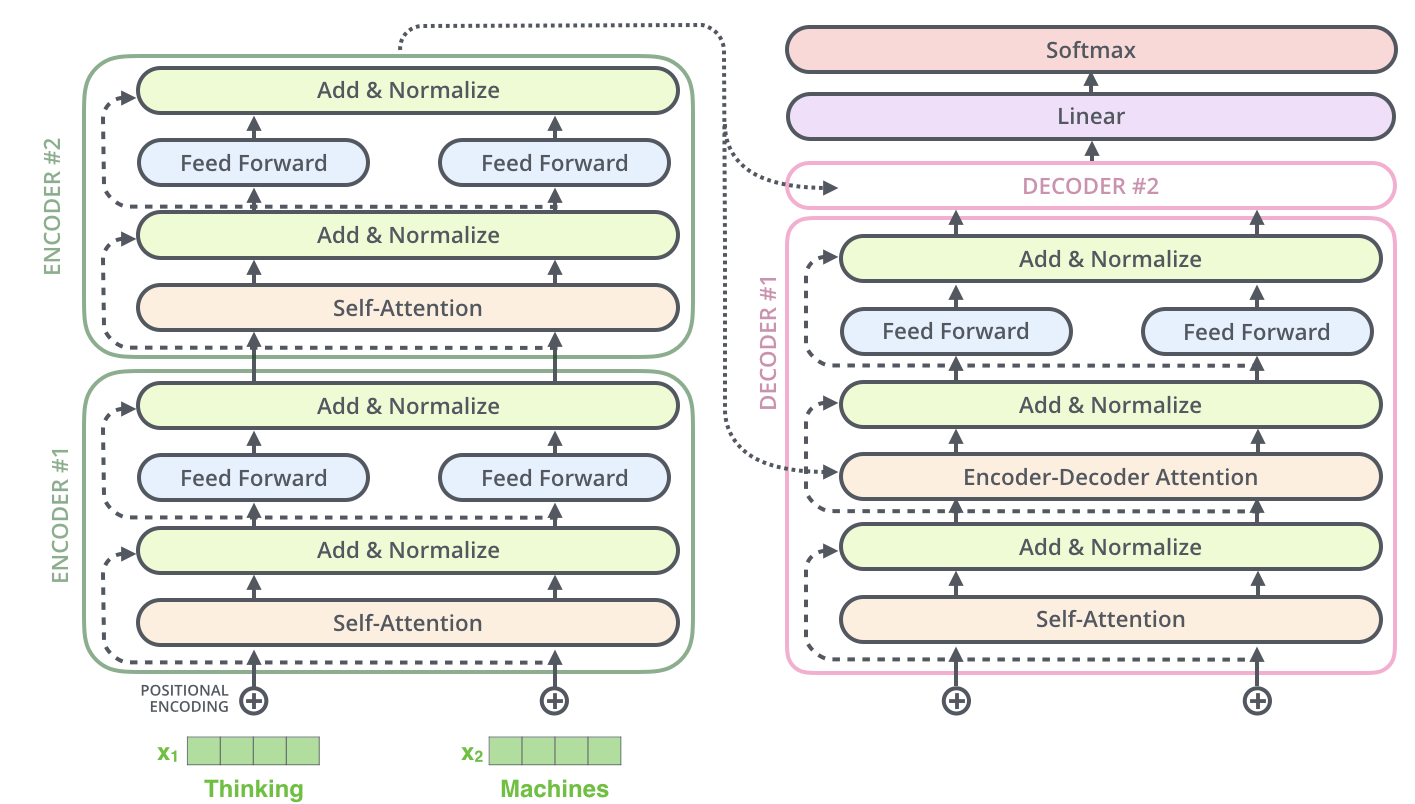
这里还有两个清楚的解释了 encoder 和 decoder 的工作方式的动画。
decoder 也由 N = 6 个相同的 layer 堆叠而成,每个 layer 由三个 sub-layer 组成:
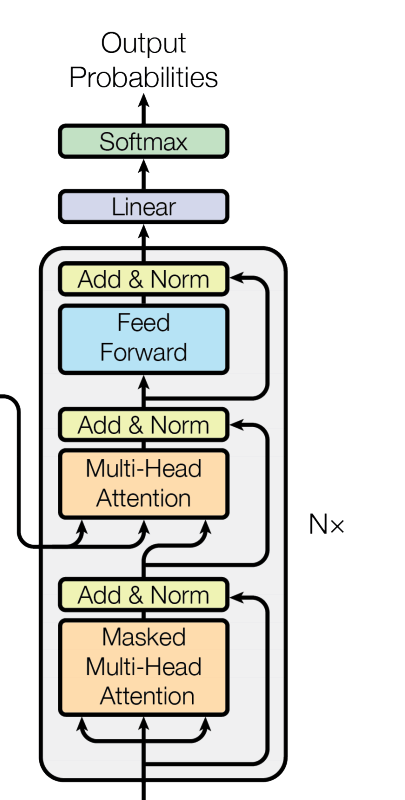
Masked Multi-Head Self-Attention
在训练时,decoder 在预测第 个位置时不应该看到未来的信息,但 self-attention 机制能让它看到全局信息(标签泄露)。所以会对在 self-attention 的 softmax 层前加 mask,将未来信息屏蔽掉。
mask 是一个下三角矩阵,对角线以及对角线左下都是 1,其余都是 0:
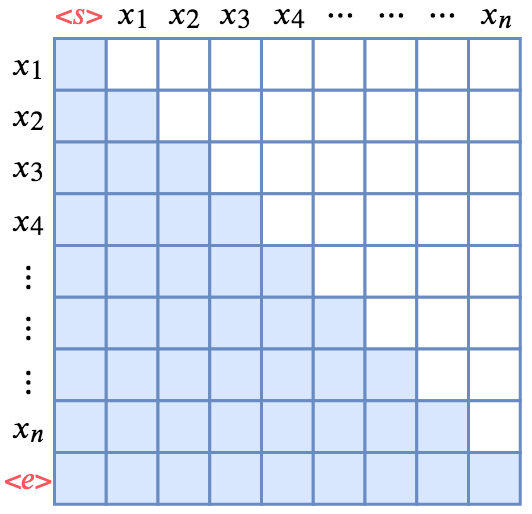
mask 矩阵,蓝色部分是 1,白色部分是 0(图片来源:从语言模型到 Seq2Seq:Transformer 如戏,全靠 Mask)
矩阵的行为当前预测到第几个单词,列为当前允许看到前几个位置的信息。然后 mask=0 的位置上的元素会都被替换为 -inf。
Multi-head Attention
即论文 3.2.3 节中的 encoder-decoder attention。它的 来自于上一位置的 decoder 的输出(第一个 layer)或上一个 decoder layer 的输出(之后的 layer),而 和 来自于 encoder 的输出。这让 decoder 的每一个位置都可以看到到输入序列的全局信息。
编码可以并行计算,但解码时,因为需要上一时刻的输出当作 ,所以无法并行计算。
Feed-Forward Network
同 encoder。
Summary
优点:
-
相比其他方法,当序列长度 小于词向量维度 时,每层的计算复杂度(complexity per layer)更低:
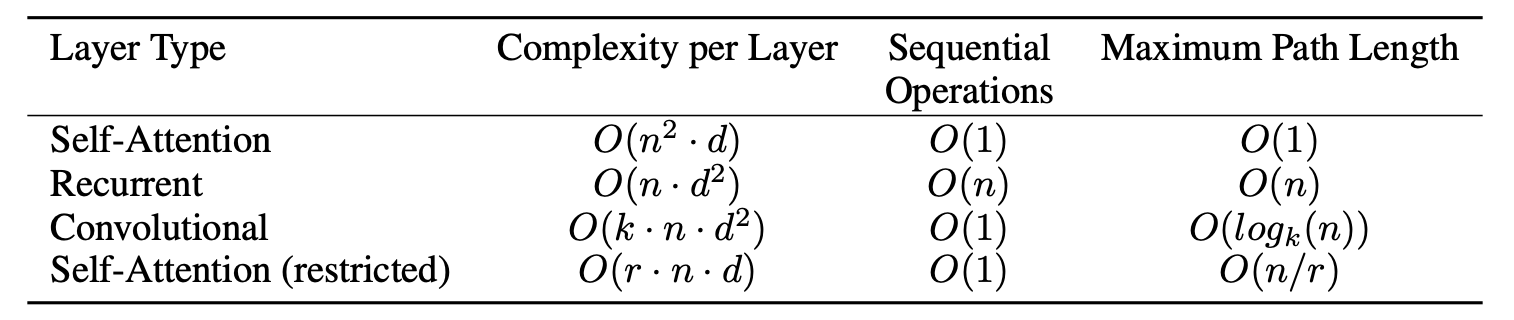
-
更好的并行性,符合目前的硬件(GPU)环境
-
更好地处理长时依赖问题:如果要处理一个长度为 n 的序列,CNN 需要增加卷积层数来扩大视野,RNN 需要从 1 到 n 逐个进行计算,而 self-attention 只需要一步矩阵运算就可以
缺点:
-
但同时从上面那张复杂度表里也能看出来,当句子太长时,Transformer 的时间复杂度是非常爆炸的。Transformer 能更好地处理长时依赖问题,但这种复杂度又让它没法处理太长的文本,即使是 Bert 的最大长度也只有 512。
于是出现了一堆致力于解决这个问题的后续工作,等我摸两天鱼再看看有没有空写这个…
-
扔掉了 RNN 和 CNN,导致失去了捕捉局部特征的能力
不过论文也提到了一个 restricted self-attention(上面那张复杂度表里有),它假设当前词只与前后 个词有关,因此只在这 个词上做 attention,复杂度是 ,相当于是在捕捉局部特征。听上去很像卷积窗口?
-
失去的位置信息非常重要,在词向量中加入 position embedding 这个解决方案依然不够好
-
非图灵完备(computationally universal)
Universal Transformer. Mostafa Dehghani, et al. ICLR 2019.