PyTorch 能有什么坏心思呢

• 名不符实的损失函数

  • NLL Loss
  • Cross Entropy Loss

• 不明觉厉的优化器实现

  • Momentum

• 奇奇怪怪的初始化器

  • Kaiming Init

记录一些 PyTorch 的细节。

#名不符实的损失函数

#NLL Loss

nn.NLLLoss，自称实现的是 Negative Log Likelihood Loss，理论上应该是：

但文档上同样也自称了，它实现的其实是：

是的 log 仅仅只存在于函数名里 (╯‵□′)╯︵╧═╧

#Cross Entropy Loss

nn.CrossEntropyLoss，理论上的交叉熵应该是：

其中 $y$ 是实际类别，$p$ 是预测类别。但文档上同样也说了，它实现的其实是 nn.LogSoftmax() + nn.NLLLoss()，即：

所以不能在用 nn.CrossEntropyLoss 前再手动 softmax 一次，不然就是两次 softmax 了，要出大问题。

#不明觉厉的优化器实现

#Momentum

Momentum 的介绍可以参考这里。首先，PyTorch 的 momentum 实现是：

而不是：

学习率是要跟整个动量相乘，而不是只乘梯度，Polyak’s Momentum 和 Nesterov’s Momentum 都是如此。

然后，Nesterov’s Momentum 的公式是：

它的思想是，先假设当前参数点 0 按上一次的动量多更新一步到点 1（下图的棕色箭头），然后在更新后的参数 $\theta'_t = \theta_t - r \rho v_{t-1}$ 上算梯度 $\nabla L(\theta'_t)$（红色箭头），用这个梯度来算这一次的动量 $v_t$（绿色箭头），最后用这个动量来真正的更新当前参数点 0 到点 2。

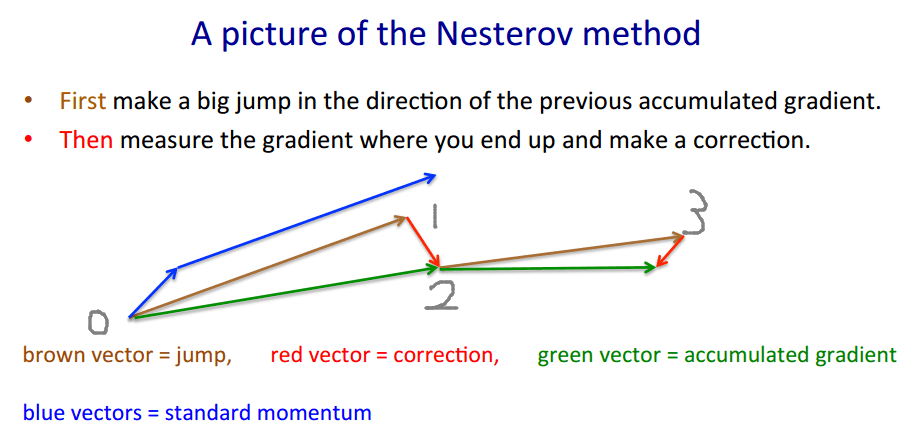
可以看到，$\theta$ 和 $\nabla L(\theta)$ 是不需要关注的，我们没有必要 $0 \rarr 1 \rarr 0 \rarr 2 \rarr 3$，我们可以直接把 $\theta'$ 和 $\nabla L(\theta')$ 作为目标，即直接 $1 \rarr 2 \rarr 3$，$1 \rarr 2$ 是在更新参数，$2 \rarr 3$ 相当于是每一步都多更新一步，就不用再假设和回退了。

那么令 $\theta_t' = \theta_t - r \rho v_{t-1}$，则有：

$- r \cdot \nabla L(\theta_t')$ 是 $1 \rarr 2$，$- r \rho v_t$ 是 $2 \rarr 3$。

包括 PyTorch 在内的深度学习框架的实现基本就是按照公式 $(1)$ 和 $(2)$ 来的，我把源码复制过来：

for i, param in enumerate(params):
    d_p = d_p_list[i]
    # l2 正则化
    if weight_decay != 0:
        d_p = d_p.add(param, alpha=weight_decay)
    if momentum != 0:
        buf = momentum_buffer_list[i]
        if buf is None:
            buf = torch.clone(d_p).detach()
            momentum_buffer_list[i] = buf
        else:
            # v_t = rho * v_{t-1} + delta L(theta'_t)
            buf.mul_(momentum).add_(d_p, alpha=1 - dampening)
        # nesterov's momentum
        if nesterov:
            # delta L(theta'_{t+1}) = delta L(theta'_t) + rho * v_t
            d_p = d_p.add(buf, alpha=momentum)
        else:
            d_p = buf
    # theta'_{t+1} = theta'_t - lr * delta L(theta'_{t+1})
    param.add_(d_p, alpha=-lr)

buf 是 $v_t$，d_p 是 $\nabla L(\theta_t')$，alpha 是动量参数 $\rho$，lr 是学习率 $r$。

#奇奇怪怪的初始化器

#Kaiming Init

PyTorch 中，linear 层和 conv 层的默认 init 是 kaiming init：

Delving Deep into Rectifiers: Surpassing Human-level Performance on ImageNet Classification. Kaiming He, et al. ICCV 2015. [Paper]

但这两个地方都给了一个奇怪的参数：

nn/modules/linear.py / nn/modules/conv.py

def reset_parameters(self) -> None:
    init.kaiming_uniform_(self.weight, a=math.sqrt(5))
    if self.bias is not None:
        fan_in, _ = init._calculate_fan_in_and_fan_out(self.weight)
        bound = 1 / math.sqrt(fan_in)
        init.uniform_(self.bias, -bound, bound)

a 这个参数看上去非常的奇怪，因为 PyTorch 在文档里说参数 a “only used with leaky_relu”。

a 代表的是 Leaky ReLU 函数 $x < 0$ 部分的斜率 negative slop。在用 kaiming uniform init 时，PyTorch 会根据这个 negative slop 算一个放缩因子 gain 出来（文档）：

然后 kaiming uniform 的边界为：

如果用别的激活函数，就不该有 negative slop 这个参数，gain 也会用别的公式计算，但 PyTorch 就是给你搞了一个 a = sqrt(5) 的奇怪的默认值。

这个问题在这两个地方有解释：

• Kaiming init of conv and linear layers, why gain = sqrt(5)
• Why the default negative_slope for kaiming_uniform initialization of Convolution and Linear layers is √5?

PyTorch 的 init 进行过一次重构（pr #9038），重构前 linear 和 conv 的默认 init 是：

def reset_parameters(self):
    stdv = 1. / math.sqrt(self.weight.size(1))
    self.weight.data.uniform_(-stdv, stdv)
    if self.bias is not None:
        self.bias.data.uniform_(-stdv, stdv)

重构之后才开始用 kaiming init。但为了保证向后兼容，他们希望重构前后的默认 init 的输出是等价的。重构前的均匀分布边界是（self.weight.size(1) 就是 fan_in（输入节点数量））：

因此为了让重构前后的边界等价：

所以这个 a = sqrt(5) 的奇怪的默认值就是这样来的，不是什么推荐值，只是为了保证向后兼容而强行设的而已…

为什么我写了那么大一段话来解释这个无聊的结论…