Self-Attention / Convolution 大锅烩
Aug 31, 2021 · 13 min · deep learning
长期记录和实现看过的各种论文里的自注意力和卷积机制,咕咕咕,实现地址在: Github
提前定义, 是一个特征,在文本任务里, 是文本长度, 是词向量维度;在视觉任务里, 是特征图的 , 是通道数量。
Attention
Self-Attenion
Attention Is All You Need. Ashish Vaswani, et al. NIPS 2017. [Paper] [Code]
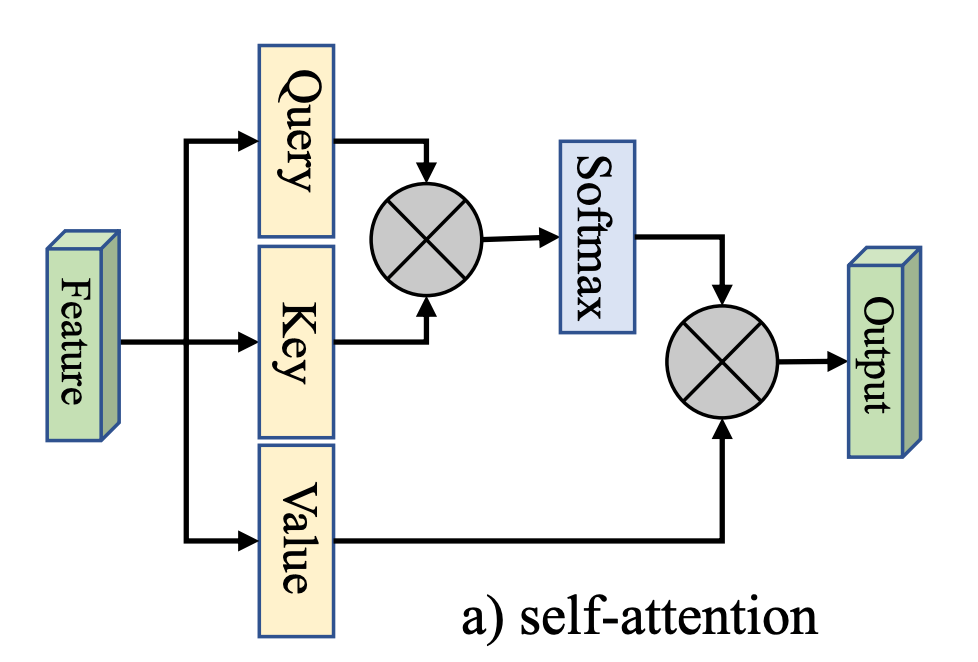
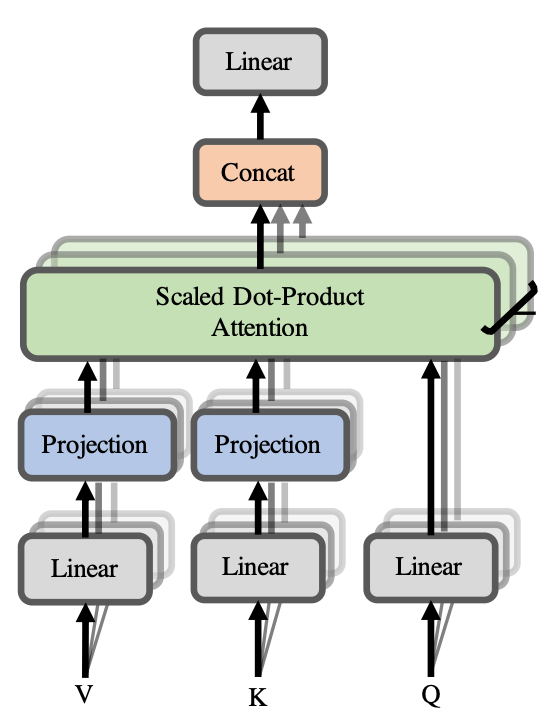
图片来源:论文 Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks
由同一个值 经过线性变换得到,然后 attention map 和 context 的计算公式为:
其中 是一个注意力头的维度, 是注意力头的数量。除以 是因为, 越大 就会越大,可能就会将 softmax 函数推入梯度极小的区域,导致更新缓慢,所以要用 对 进行缩放。
最后 会经过线性层、残差连接和 Layer Normalization。
一个简化版本是,把线性变换扔掉,直接用 计算 attention,即 ,从而省掉那三个线性层的计算量:
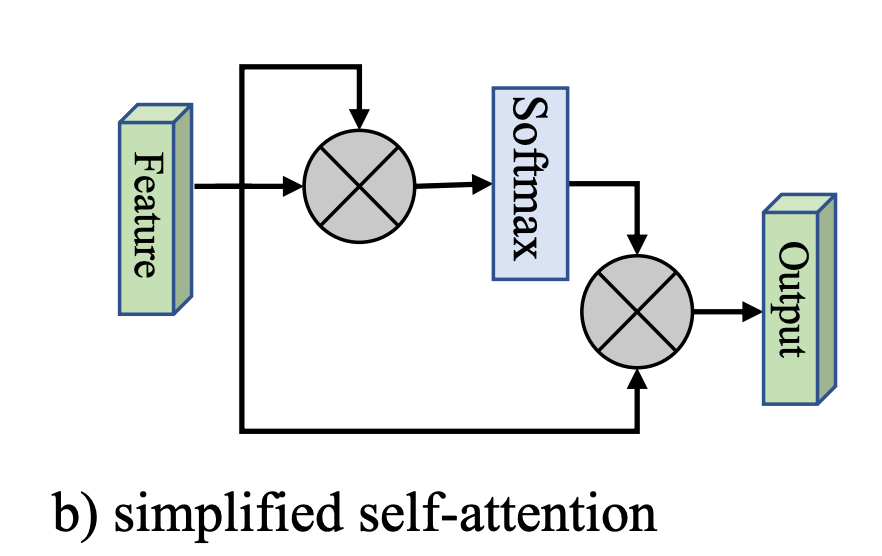
图片来源:论文 Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks
Self Attention 是在计算任意两个位置之间的相关性,得到一个 的 attention map,所以计算复杂度是 (“简化版本”也是这样),这是一个很高的计算开销。所以 Bert 的最大长度只有 。而对于视觉任务来说,,所以特征图也不能太大,一般 和 都需要先被降到 10+ 的数量级。
SAGAN
Self-Attention Generative Adversarial Networks. Han Zhang, et al. ICML 2019. [Paper] [Code]
SAGAN 是一个用 self-attention 来替代了卷积层的 GAN,它的 self-attention 跟原始 transformer 的 self-attention 的不同在于:
- 在将 通过线性变换得到 和 时,进行了降维()
- 在残差连接之前,对 进行了缩放:,其中 是一个可学习的参数
External Attention
Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks. Han Zhang, et al. arXiv 2021. [Paper] [Code]
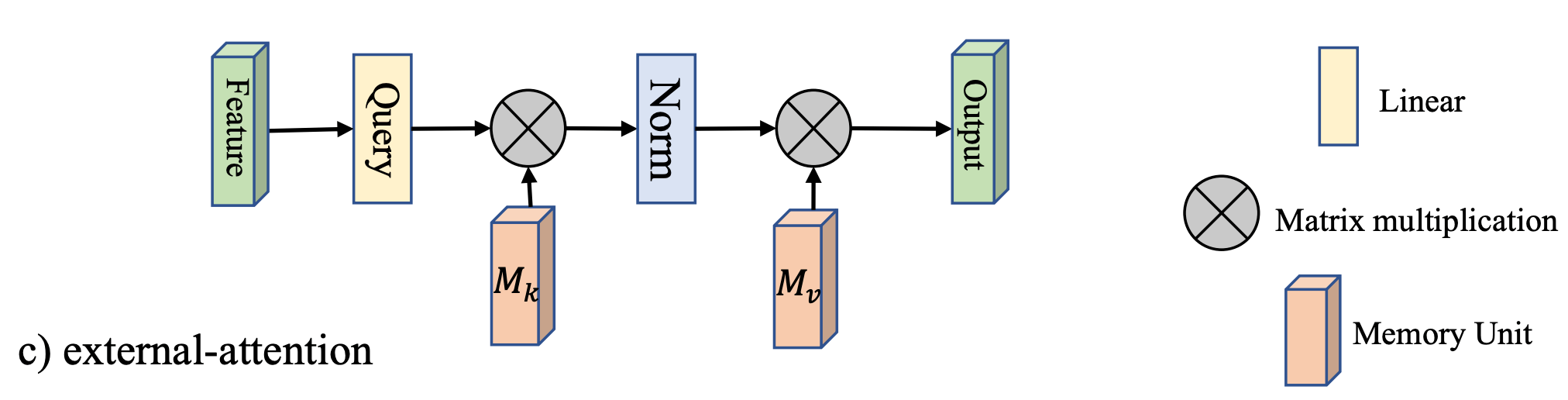
图片来源:论文 Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks
External Attention 主要考虑了以下问题:
- 原始 self attention 会计算任意两个位置(pixel)之间的相关性,计算量太大。但实际上,attention map 是很稀疏的,只有很少量的 pixel 之间有关联,所以没有必要用 的 attention map
- 原始 self attention 只考虑了同一个样本中不同 pixel 之间的关系,但没有考虑不同样本间的关联
因此 External Attention 提出用 external memory unit 和 (都是可学习的参数)来代替 和 :
其中 , 是一个超参。
对于第一个问题, 的复杂度来源于 的矩阵相乘,而这里 的维度从 变成了 ,因此复杂度变为了 ,与 线性相关。因为 可以取得远远小于 (在论文的实验中, 的时候效果就已经很好了),所以计算复杂度可以降低很多。
对于第二个问题,可以认为 external memory unit 学习到了整个数据集的信息,因此考虑了不同样本间的关联。
式 中的 是 double-normalization 操作。Softmax 只会对一个维度进行归一化,但 attention map 对于输入特征的 scale 比较敏感,所以 double-normalization 在 softmax 之后对另一个维度也进行了归一化:
Fastformer
Fastformer: Additive Attention Can Be All You Need. Chuhan Wu, et al. arXiv 2021. [Paper] [Code]
又是『XXX is all you need』系列的题目,让人审美疲劳。虽然这个题目包含了它应该包含的信息:“比原始 Transformer 快,因为我们用了 additive attention”,但还是让人审美疲劳。
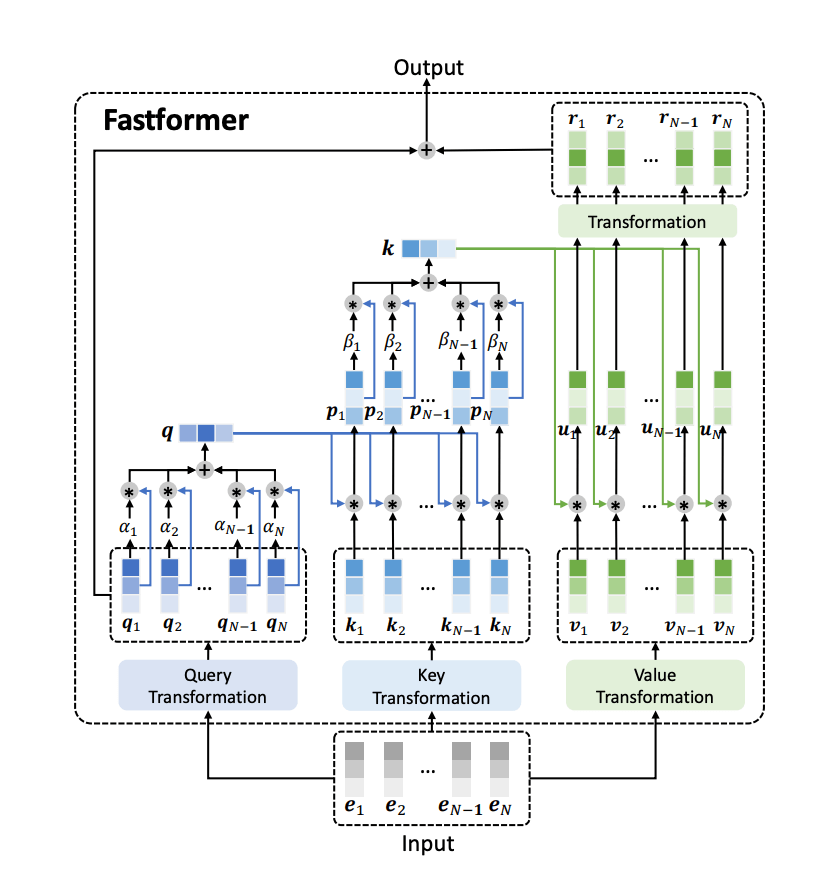
同样是想解决 的稀疏 attention map 带来的高计算量的问题。它的处理方式是先用 additive attention 把 融合成了一个 global query vector :
其中 (这里直接把 维降到了 1 维)。然后用 和 矩阵 element-wise 相乘,乘完之后再用和上面一样的 additive attention 得到一个向量 :
最后用 和 矩阵相乘,得到最终的输出:
因为有 additive attention 这个降维操作,所以上面每一个矩阵乘法的复杂度都是 ,element-wise 乘法的复杂度也是 ,所以总的时间复杂度是线性的 。
HaloNets
Scaling Local Self-Attention for Parameter Efficient Visual Backbones. Ashish Vaswani, et al. CVPR 2019. [Paper]
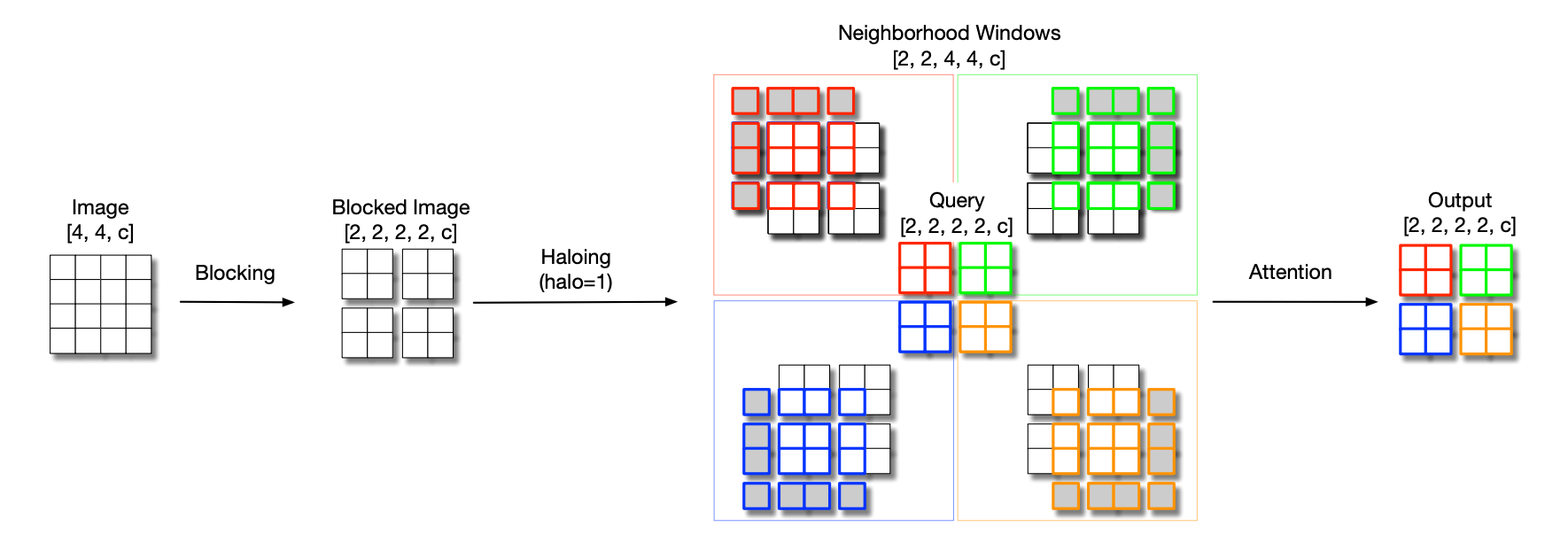
图片来源:论文 Scaling Local Self-Attention for Parameter Efficient Visual Backbones
用 self-attention 来做类似于卷积的操作,心路历程是:
- 如果用全局 self-attention,计算量太大;如果用卷积中的滑动窗口,在每个窗口里做 local self-attention,由于每个窗口的结果都要一直存在显存里没法释放,容易造成显存溢出
- 但卷积中,两个相邻的滑动窗口中的大部分元素都是一样的,为了减少这部分重复的计算量,论文直接将输入的特征图分成了不重复的一些 block(上图中的 blocked image),然后在每个 block 里做 local self-attention,所以论文管这个操作叫 blocked local self-attention
- 但只在 block 里做 self-attention 也是不合适的,周边共享的元素多少也要考虑一些,因此论文在每个窗口边上都 pad 了一圈(上图中的 neighborhood windows 周边那圈五颜六色的东西),以增加感受野。因为 pad 的这一圈看上去很像光环,所以论文管这个操作叫 haloing
Linformer
Linformer: Self-Attention with Linear Complexity. Sinong Wang, et al. arXiv 2020. [Paper]
从实现上来看,和原始 Transformer 的区别就是,对 用 进行了降维(上图中的 Projection),即:
是一个超参常数,所以时间复杂度降到 。同时它还使用了一些参数共享的 trick 来进一步降低计算量。
但论文还证明了为什么可以用 来近似原始的 attention map (虽然我觉得略显强行)。原文的 Theorem 2 先证明了当 时,一定存在 使得 可以近似 。这里 的取值与 有关,复杂度还不是线性。但如果考虑到 这一点(我还没搞明白这一点是怎么来的), 的选择就可以独立于 ,从而变为线性复杂度。
Convolution
Selective Kernel
Selective Kernel Networks. Xiang Li, et al. CVPR 2019. [Paper] [Code]
希望能够自适应地调整感受野的大小,为了做到这一点,论文采取的方式是用多个大小不同的卷积核生成特征图,然后把这些特征图融合在一起。
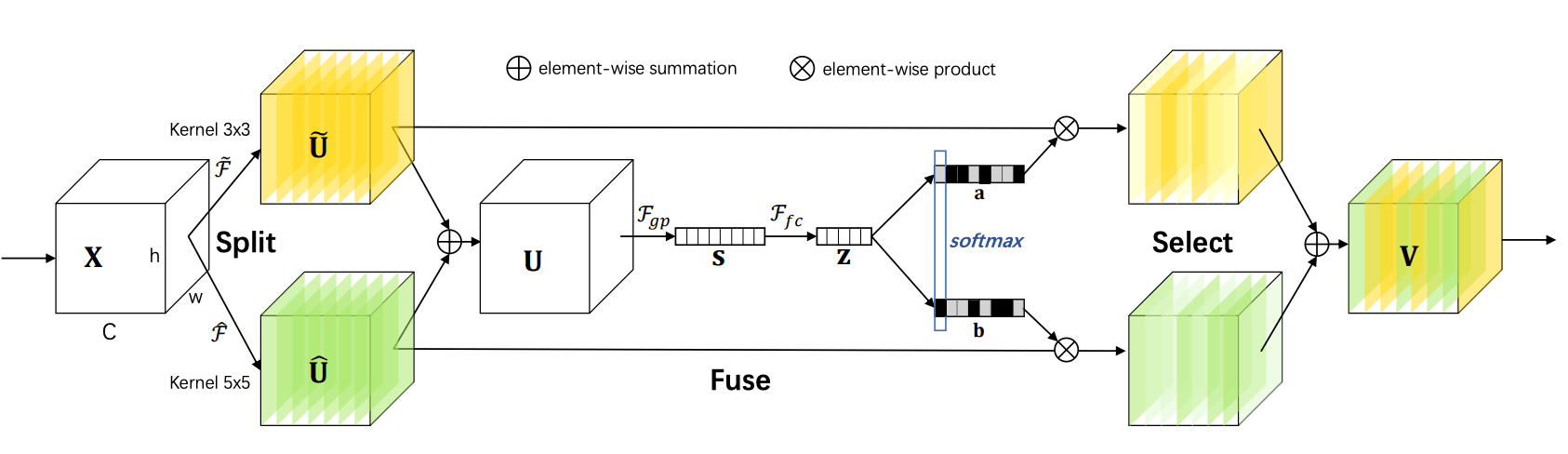
图片来源:论文 Selective Kernel Networks
- Split:用 个大小不同的卷积核生成特征图,上图中举的是 和 两个卷积核的例子
- Fuse:把不同卷积核生成的特征图相加,然后经过平均池化 全连接 Batch Norm ReLU,得到一个特征向量 ,其中 , 都是超参,用于控制通道维度
- Select:用 来计算一个 attention map,然后把 个特征图加权求和,得到最终的输出
Squeeze-and-Excitation
Squeeze-and-Excitation Networks. Jie Hu, et al. CVPR 2018. [Paper] [Code]
赋予不同通道不同的权重,这样就可以加强重要的通道特征。
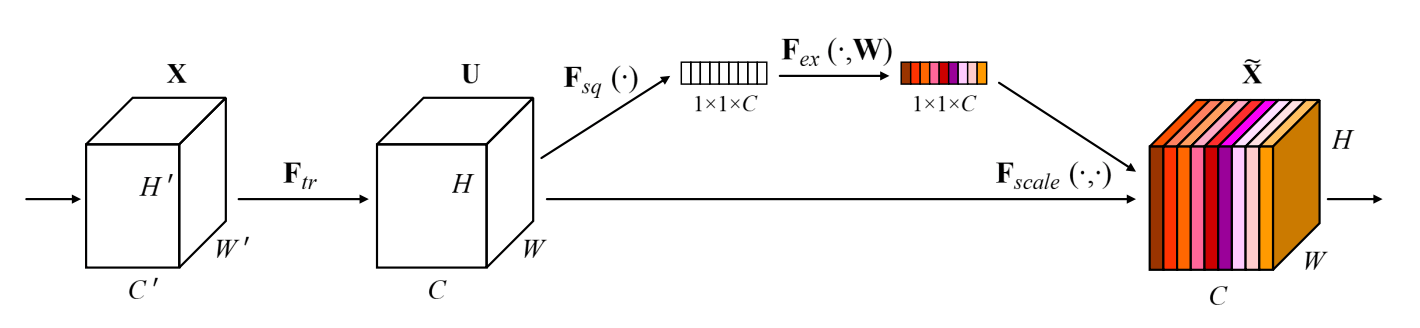
图片来源:论文 Squeeze-and-Excitation Networks
通道权重的计算方式是:
-
Squeeze:先把卷积出的特征图 平均池化成一个向量 ,这一步抽离了空间上的信息,这样后面就可以只关注通道之间的关系
-
Excitation: 只能体现在当前 batch 上计算出来的通道关系,所以论文加了两个全连接层来利用整个数据集的信息:
其中 是 ReLU 激活函数, 和 是两个全连接层, 是最终各个通道的权重
最后把特征图 跟权重 相乘就行。
Involution
Involution: Inverting the Inherence of Convolution for Visual Recognition. Duo Li, et al. CVPR 2021. [Paper] [Code]
普通的卷积有两个特点:空间不变(spatial-agnostic)(不同空间位置共享同一个卷积核)和通道特异(channel-specific)(不同通道对应不同的卷积核)。参数数量为 ,其中 分别为输入和输出通道数量,以及卷积核大小。
而这篇论文认为:
- 由于通道数量 往往成百上千,所以为了限制参数量和计算量, 的取值往往较小,从而限制了感受野大小
- 空间不变的特征可能会剥夺卷积核适应不同空间位置的能力
- 卷积核在通道维度往往存在冗余,即很多卷积核是近似线性相关的。也就是说,如果把每个输出通道对应的卷积核铺成一个 大小的矩阵,那么矩阵的秩不会超过 。所以缩减卷积核的通道维度可能并不会明显影响效果
因此论文提出了一种跟卷积相反的 involution 操作:空间特异(不同空间位置对应不同的卷积核)和通道不变(不同通道共享同一个卷积核),参数数量为 , 表示 个输入通道分成 组(每组 个通道),每组通道共享同一个卷积核。
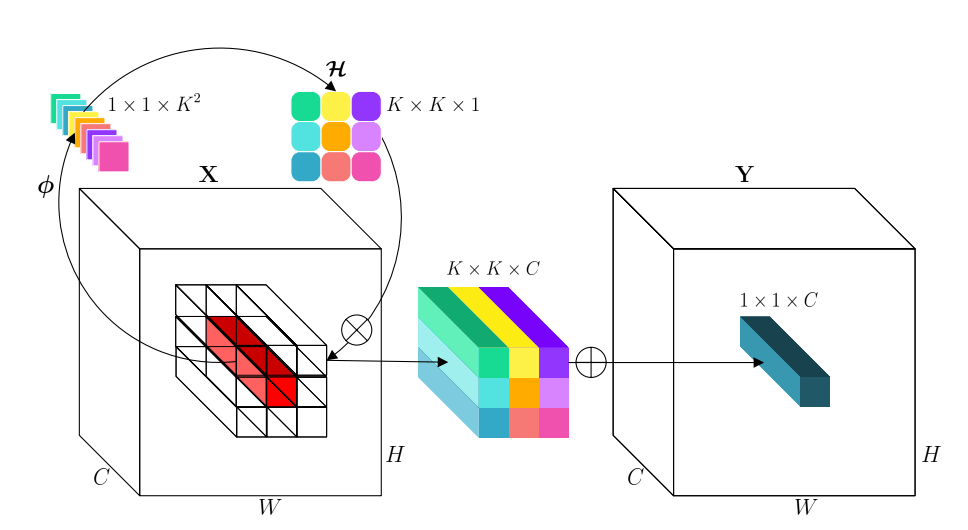
图片来源:论文 Involution: Inverting the Inherence of Convolution for Visual Recognition
和卷积不一样的是,involution 的核是根据输入的特征图自动生成的,一个通用的形式是:
其中 表示坐标 的某个邻域上的坐标集合, 表示 对应的特征。在实例化这个形式时,论文用了比较简单的方式,即令 这个单点,然后:
论文另一个挺有意思的地方是,它指出 self-attention 公式也可以用这个式子来表示,即:
其中 是 query 对应的 key 的范围。