p-value

• P 值 (p-value)
• 卡方 (chi-square)
• 卡方分布 (chi-square distribution)
• 总结

一个例子：一个正常的硬币，在被投掷无数次后，结果一定会是正面朝上和反面朝上各占 50%。如果想要知道一个硬币是否正常，是否被做过手脚，显然是没办法投掷无数次的。因此，只能用有限的结果来判断“该硬币是否正常”。

#P 值 (p-value)

在统计学上，通常会设定一个虚无假设（零假设，Null Hypothesis），记作 $H_0$。和一个与虚无假设对立的对立假设（Alternative Hypothesis），记做 $H_1$。如果证明虚无假设错误，则可以推出对立假设成立。

本例中：

• $H_0$ : 该硬币是正常硬币
• $H_1$: 该硬币被做过手脚

p-value：错误拒绝（reject）$H_0$ 假设的概率，即 $H_0$ 事实上成立，但我们计算出的结果却错误判断虚无假设不成立的概率。

#卡方 (chi-square)

我们认为该硬币是正常硬币，因此我们对于投掷 10 次硬币的期望值 (expected value) 是正面 5 次，反面 5 次。而实际结果是正面 3 次，反面 7 次，这个结果就是我们对于投掷 10 次硬币的观测值（observed valued）。

通过分析期望值和观测值的差距，就可以判断出硬币是否正常，而这个期望值和观测值差距的判断方法就是 chi-square，公式为：

$$x^2 = \sum_{i=1}^{n} \frac{(O_i-E_i)^2}{E_i}$$

$O$ 为观测值，$E$ 为期望值。可以看到该公式与方差很相似，方差是一组数据与其均值的比较，而 chi-suaqre 是一组数据与另一组数据期望值的比较。

本例中，$\text{chi-square} = \frac{(3-5)^2}{5} + \frac{(7-5)^2}{5} = 1.6$

#卡方分布 (chi-square distribution)

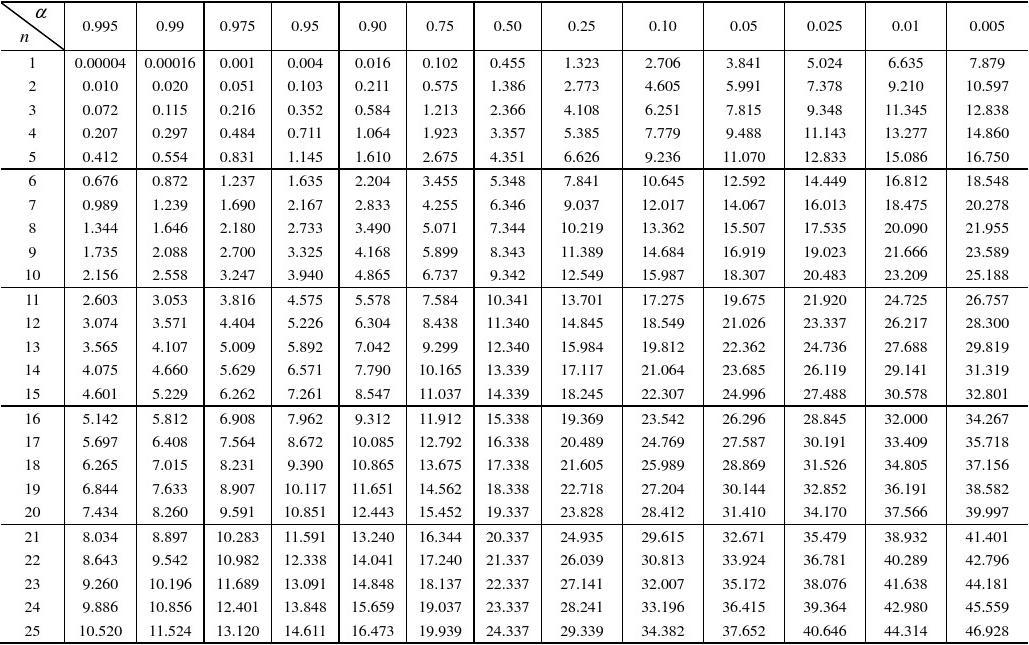
上图为卡方分布表，$\alpha$ 为错误拒绝 $H_0$ 假设的概率，$n$ 为自由度，即独立变量数减 1。本例中，独立变量数为 2（正面和反面），所以自由度 $n = 1$。

当置信度为 95%，即错误拒绝 $H_0$ 的概率为 0.05，意义就是我们有 95%的概率确信检验结果正确，有 5% 的概率会错误拒绝虚无假设。（所以大多数时候用 $\text{p-value}<0.05$ 来判断结果是否靠谱，当然根据情况也可以不用 0.05）

本例中，对照着卡方分布表，找到 $n = 1$ 所在的行，发现 1.6 介于 1.323 和 2.706 之间，查出其 p-value 介于 0.25 到 0.1 之间，大于 0.05。所以我们不能拒绝 $H_0$，即 $H_0$ 成立，该硬币是正常硬币。

可以看到，当自由度相同，chi-square 越大，其 p-value 越小。因为如果观测值与期望值越一致，则说明检验现象与 $H_0$ 越接近，则越没有理由拒绝 $H_0$。如果观测值与期望值越偏离，说明 $H_0$ 越站不住脚，则越有理由拒绝 $H_0$，从而推出对立假设的成立。

一个极端的例子，如果掷 10 次硬币，刚好 5 次正面朝上 5 次反面朝上，此时 $\text{chi-square} = 0$，p-value 远大于 0.095，没有理由拒绝 $H_0$，即 $H_0$ 成立，该硬币是正常硬币。

#总结

做出 $H_0$，$H_1$ 这对互斥的假设，计算出 $H_0$ 为真时的期望值和实际观测值，通过期望值和观测值求得 chi-square，再通过查卡方分布表得到 p-value，然后将 p-value 与 $\alpha$（1 - 置信度）比较，如果 $\text{p-value} < \alpha$，则拒绝 $H_0$，推出 $H_1$ 成立，否则接受（accpet）$H_0$，推出 $H_1$ 不成立。

大部分时候 p-value 用于检验独立变量与输入变量的关系，$H_0$ 假设通常为假设两者没有关系，所以若 $\text{p-value} < 0.05$，则可以推翻 $H_0$（两者没有关系），推出 $H_1$（两者有关系），我们就说这个独立变量重要（significant），因为这个独立变量与输出结果有关系。